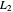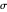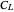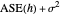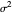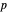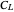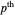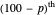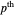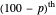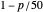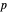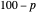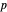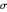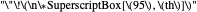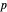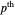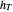Nonparametric Regression and Kernel Smoothing: Confidence Regions for the L2-Optimal Curve Estimate

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
This Demonstration considers one of the simplest nonparametric-regression problems: how to "optimally denoise" a noisy signal, assuming it is a smooth curve plus a realization of i.i.d. centered Gaussian variables of known variance 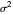 . The setting is the same as in the Demonstration "Nonparametric Curve Estimation by Kernel Smoothers: Efficiency of Unbiased Risk Estimate and GCV Selectors". Recall that applying a classical kernel-smoothing method to a noisy signal actually produces a trajectory of candidate estimates of the underlying curve, each estimate being associated with (or tuned by) a bandwidth value, denoted
. The setting is the same as in the Demonstration "Nonparametric Curve Estimation by Kernel Smoothers: Efficiency of Unbiased Risk Estimate and GCV Selectors". Recall that applying a classical kernel-smoothing method to a noisy signal actually produces a trajectory of candidate estimates of the underlying curve, each estimate being associated with (or tuned by) a bandwidth value, denoted  . Ideally one would like to pick "the optimal
. Ideally one would like to pick "the optimal  " given the data. A classical approach is to attempt (as in the previously mentioned Demonstration) to minimize over
" given the data. A classical approach is to attempt (as in the previously mentioned Demonstration) to minimize over  the average of the squared errors
the average of the squared errors 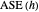 , which is a discrete version of the
, which is a discrete version of the 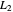 distance between the underlying (true) curve and the curve estimate obtained with
distance between the underlying (true) curve and the curve estimate obtained with  (see Details). The unknown true minimizer (resp. the associated curve estimate) is called the ASE-optimal bandwidth (resp. the
(see Details). The unknown true minimizer (resp. the associated curve estimate) is called the ASE-optimal bandwidth (resp. the 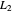 -optimal curve estimate).
-optimal curve estimate).
Contributed by: Didier A. Girard (March 2013)
(CNRS-LJK and University Joseph Fourier, Grenoble)
Open content licensed under CC BY-NC-SA
Snapshots
Details
See the Demonstration "Nonparametric Curve Estimation by Kernel Smoothers: Efficiency of Unbiased Risk Estimate and GCV Selectors" for the definitions of the setting and the 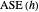 distance when a noisy signal is given. In that Demonstration, the now classical cross-validation (identical to GCV here) choice in the family of candidate curve estimates is computed and compared with the curve estimate using the ASE-optimal bandwidth.The
distance when a noisy signal is given. In that Demonstration, the now classical cross-validation (identical to GCV here) choice in the family of candidate curve estimates is computed and compared with the curve estimate using the ASE-optimal bandwidth.The  value that minimizes the unbiased risk estimate Mallows'
value that minimizes the unbiased risk estimate Mallows' 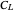 (also denoted UBR) is also computed and it proves to be very close to the GCV choice in many cases.
(also denoted UBR) is also computed and it proves to be very close to the GCV choice in many cases.
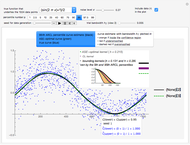
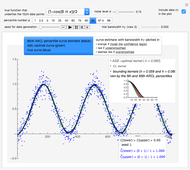
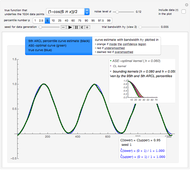
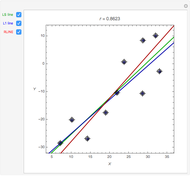
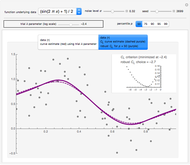
Snapshot 1: Selecting 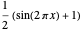 as the true function underlying the data, setting
as the true function underlying the data, setting 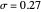 , and using the
, and using the  and
and 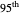 percentiles as lower and upper bounds (select
percentiles as lower and upper bounds (select 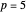 or
or  , with the only difference that the plotted ARCL percentile curve estimate is either the one associated with the lower bound or the upper bound), we can find after a few hundreds of simulations that the empirical values
, with the only difference that the plotted ARCL percentile curve estimate is either the one associated with the lower bound or the upper bound), we can find after a few hundreds of simulations that the empirical values 
 and
and 
 (not shown here) converge respectively to 97.2 and 94.8, which means that the coverage probability is very close the nominal coverage probability 0.95 for the upper bound and slightly conservative for the lower bound.
(not shown here) converge respectively to 97.2 and 94.8, which means that the coverage probability is very close the nominal coverage probability 0.95 for the upper bound and slightly conservative for the lower bound.
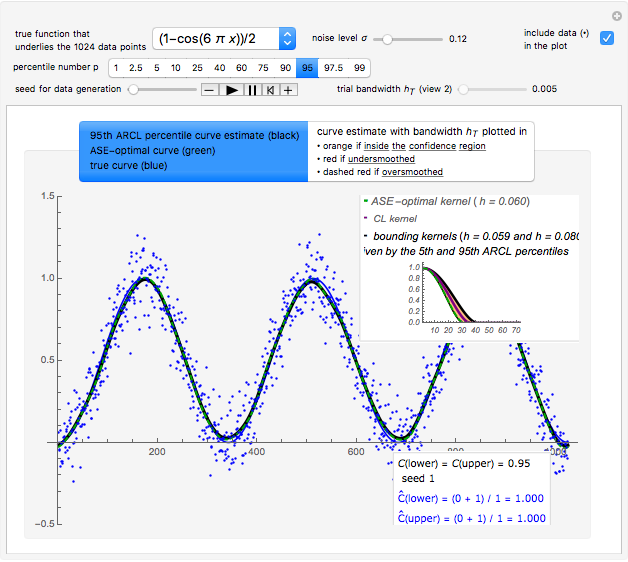
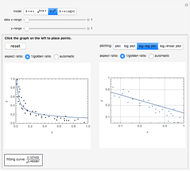
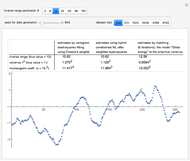
Snapshot 2: Selecting 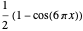 as the true function, setting
as the true function, setting 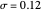 , and still selecting
, and still selecting 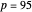 , we could find after enough simulations that the two empirical values
, we could find after enough simulations that the two empirical values 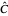
 converge to values close to 0.95 (even more than in the above case), but furthermore, during this simulation, we can see in the top inset of this first view that the two kernels associated with the lower bound and the upper bound are quite close for any seed.
converge to values close to 0.95 (even more than in the above case), but furthermore, during this simulation, we can see in the top inset of this first view that the two kernels associated with the lower bound and the upper bound are quite close for any seed.
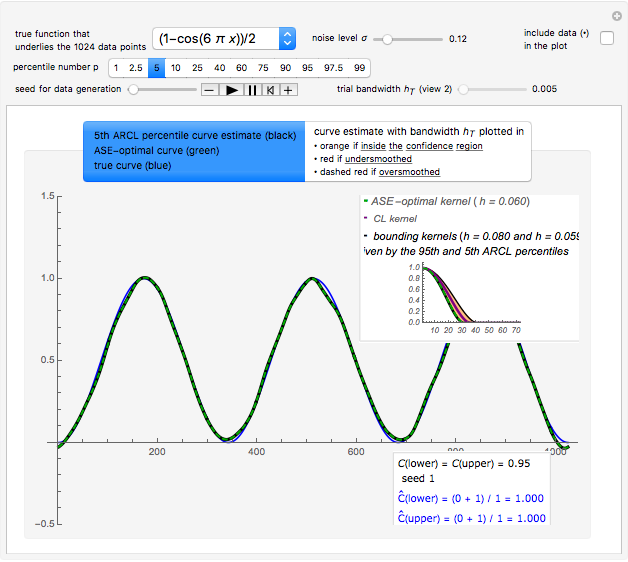
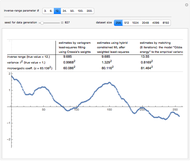
Snapshot 3: As in Snapshot 2, after having stopped the simulation by clicking the pause button and selecting 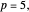 the curve estimate associated with the
the curve estimate associated with the 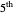 percentiles is now plotted instead of the one associated with the
percentiles is now plotted instead of the one associated with the 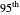 (plotted in black): an important observation (perhaps more important than the closeness of the kernels mentioned above) is that this
(plotted in black): an important observation (perhaps more important than the closeness of the kernels mentioned above) is that this 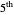 ARCL percentile curve estimate is almost indistinguishable from the ASE-optimal curve estimate as was also the case for the
ARCL percentile curve estimate is almost indistinguishable from the ASE-optimal curve estimate as was also the case for the 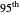 ARCL percentile curve estimate. This can be observed for almost every seed (the seed is 1 in this snapshot), albeit with sometimes small local fluctuations. This means that for such a setting, one can get a rather accurate plot of the unknown ASE-optimal curve estimate with a confidence level of 0.90.
ARCL percentile curve estimate. This can be observed for almost every seed (the seed is 1 in this snapshot), albeit with sometimes small local fluctuations. This means that for such a setting, one can get a rather accurate plot of the unknown ASE-optimal curve estimate with a confidence level of 0.90.
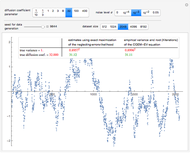
Snapshot 4: Selecting the "bell + peak" function as the true function, setting 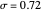 , choosing a large noise level, and still selecting
, choosing a large noise level, and still selecting 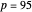 , we could find after enough simulations that the empirical values
, we could find after enough simulations that the empirical values 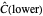
 and
and 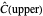
 converge respectively to 0.939 and 0.940, so the coverage error is small; however, for almost any seed, we can see that the
converge respectively to 0.939 and 0.940, so the coverage error is small; however, for almost any seed, we can see that the 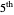 ARCL percentile curve estimate and the
ARCL percentile curve estimate and the 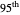 ARCL percentile curve estimate are quite different.
ARCL percentile curve estimate are quite different.
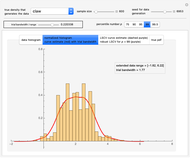
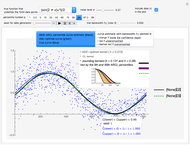
Snapshot 5: As in Snapshot 4, having stopped the previous simulations, you can observe that, even if the peak seems to be present in this second view when using a small bandwidth (shown here for seed set to 1), the upper bound at level 0.95 (whose computed value 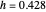 is displayed in the top inset of the first view) yields a curve estimate where the peak is not present.
is displayed in the top inset of the first view) yields a curve estimate where the peak is not present.
(This curve estimate is obtained in the second view by moving the slider "trial bandwidth" toward  or by noticing that it automatically takes the dashed red appearance as soon as the bandwidth exceeds 0.428.)
or by noticing that it automatically takes the dashed red appearance as soon as the bandwidth exceeds 0.428.)
With such data with a lot of noise, this methodology does not permit us to guarantee, at a confidence level of 0.95, the existence of this peak; nevertheless, the global "bell-like" shape is well guaranteed. However, it could be checked that with a lower noise level (e.g.  as in the thumbnail), the confidence regions at level 0.95 that can be displayed in this second view do consist of curve estimates where the peak is almost always present.
as in the thumbnail), the confidence regions at level 0.95 that can be displayed in this second view do consist of curve estimates where the peak is almost always present.
Reference
[1] D. A. Girard, "Estimating the Accuracy of (Local) Cross-Validation via Randomised GCV Choices in Kernel or Smoothing Spline Regression," Journal of Nonparametric Statistics, 22(1), 2010, pp. 41–64. doi:10.1080/10485250903095820.
Permanent Citation