Mathematica MathWorld Wolfram Science More »

Estimating Conditional Expectations with Monte Carlo Simulation and Least Squares Regression


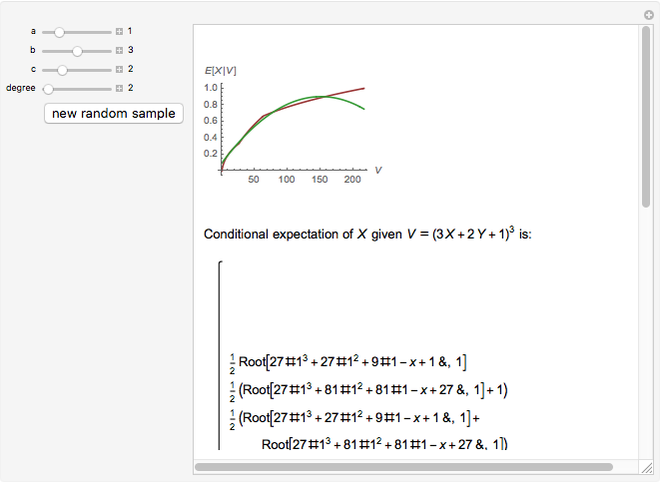
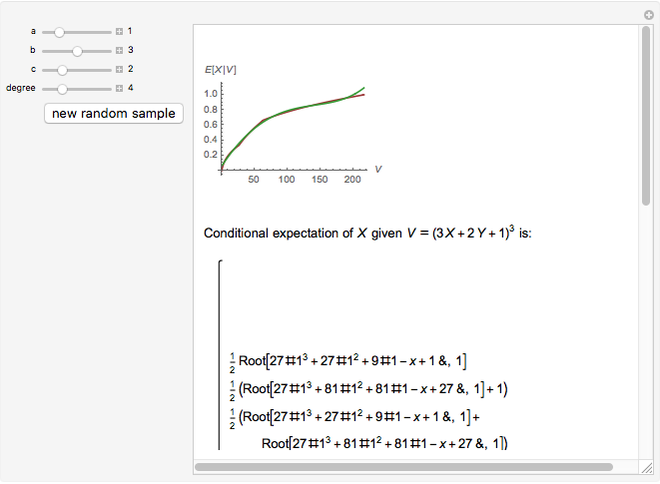
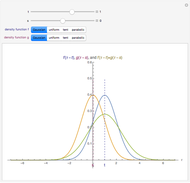
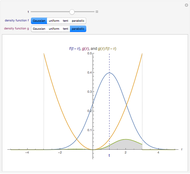
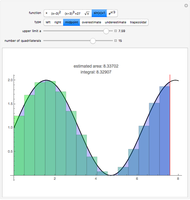
	In this Demonstration we consider three random variables, and , which are uniformly distributed on the interval [0,1] and , where , , and are (user-specified) non-negative integers. The purpose is to compute the conditional expectation symbolically and by polynomial regression on data obtained from randomly generated sequences (, ). The display shows the graphs of the conditional expectation function (red) and an estimate (green), explicit formulas giving the exact value of the conditional expectation and its polynomial estimate, and the (square-integrable) error of the estimate, obtained by integrating the square of the difference between the true conditional expectation and the estimated one. Use the controls to choose the values of , , and and the degree of the polynomial to be used in the regression.


	Contributed by: Andrzej Kozlowski
	Show Initialization Code

Many problems in science, economics, finance, and so on require us to compute conditional expectations. If

and

are

random variables with nice density, then the conditional expectation

can be defined as the orthogonal projection of

on the linear subspace space of all functions of

in Hilbert space of all

(square-integrable) random variables. Thus the conditional expectation can be though of as a function of

with the minimum

distance from

. This justifies the well-known Monte Carlo method of approximating

by generating a sample of (

) pairs and regressing

by solving a least-squares problem for a polynomial of some chosen degree. In this Demonstration we start with two independent random variables

and

with uniform distribution on [0,1]. As

we take a random variable

for some positive integers

, and

. In this case Mathematica is able to compute the exact formula for

, so that we can assess the accuracy of the estimate by computing the

norm using numerical integration.

The idea of this Demonstration is based on an example in chapter 11.6 of

K. L. Judd, Numerical Methods in Economics, Cambridge, MA: The MIT Press, 1998.

Report an issue »

	Source page:
	Email	Name (optional)
	Occupation (optional)	Organization (optional)
	I use Mathematica often occasionally never
	Country (optional) Remember me
	Note: Please do not include anything you consider confidential or proprietary. Your message and contact information may be shared with the author of any specific Demonstration for which you give feedback, but will not otherwise be published or distributed. Privacy Policy »

RSS

Atom