Fresnel Equations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
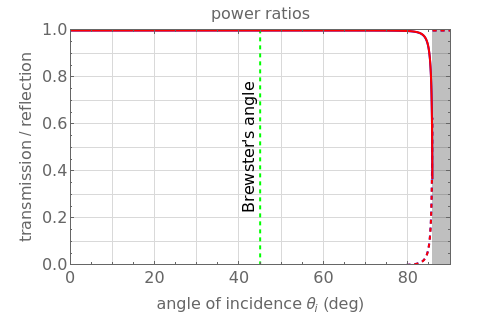
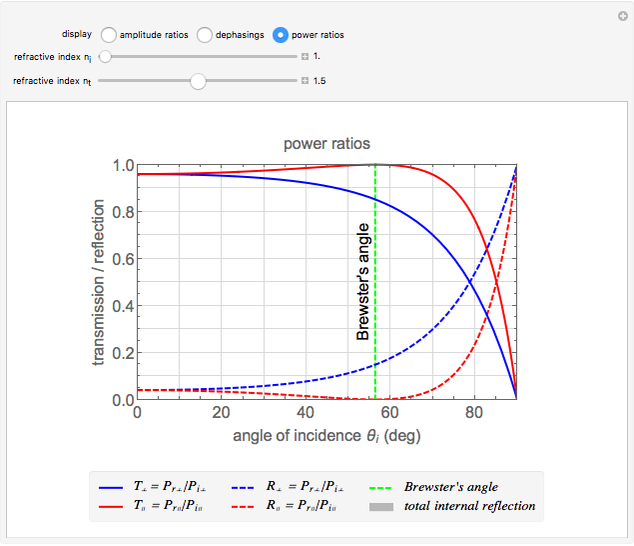
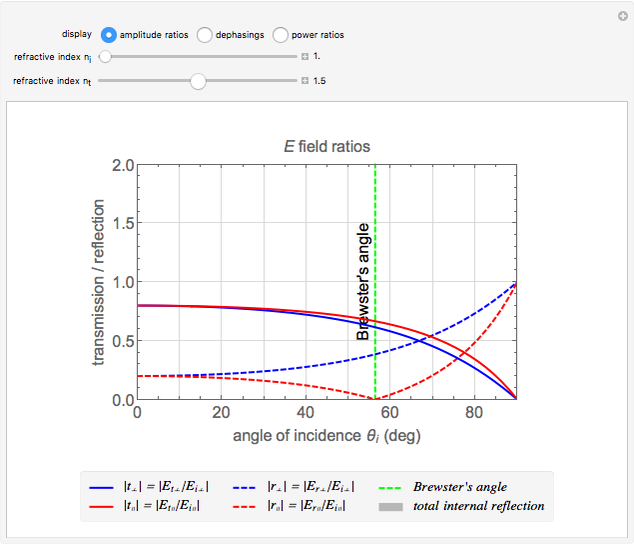
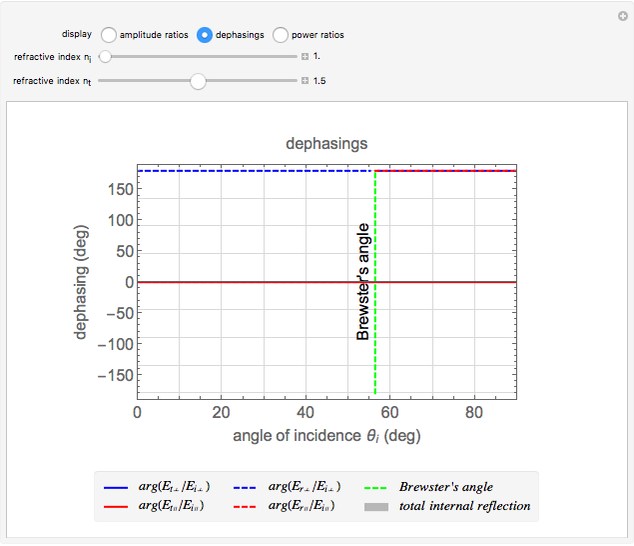
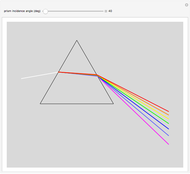
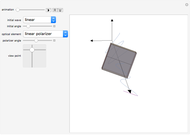
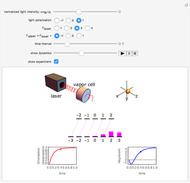
Fresnel equations describe how light is transmitted and reflected when crossing the interface between two dielectric media of differing indices of refraction. This Demonstration shows how the transmission and reflection coefficients both depend on the angle of incidence  between the light beam and the normal to the interface and on the light polarization, which can be either parallel (∥) or perpendicular (⊥) to the plane of incidence. You can display either the electric field amplitude ratios and their dephasings, or the power ratios. You can change the refractive indices of the first
between the light beam and the normal to the interface and on the light polarization, which can be either parallel (∥) or perpendicular (⊥) to the plane of incidence. You can display either the electric field amplitude ratios and their dephasings, or the power ratios. You can change the refractive indices of the first  ) or second
) or second  ) medium and observe how the coefficients change. When
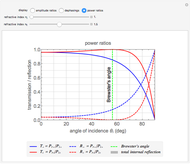
) medium and observe how the coefficients change. When  , reflection increases at large angles and tends to 1 for 90°. When
, reflection increases at large angles and tends to 1 for 90°. When  , you observe total internal reflection when the angle of incidence is bigger than the critical angle
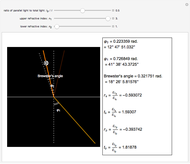
, you observe total internal reflection when the angle of incidence is bigger than the critical angle  . In this case, all the power is reflected and the transmitted field is an evanescent wave (instead of a traveling wave). Another angle of interest is Brewster's angle
. In this case, all the power is reflected and the transmitted field is an evanescent wave (instead of a traveling wave). Another angle of interest is Brewster's angle  , for which light with parallel polarization is fully transmitted; thus reflected light will be polarized perpendicularly to the plane of incidence whatever the polarization of incoming light.
, for which light with parallel polarization is fully transmitted; thus reflected light will be polarized perpendicularly to the plane of incidence whatever the polarization of incoming light.
Contributed by: Gianni Di Domenico (Université de Neuchâtel) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Fresnel equations for the transmission and reflection of light with parallel polarization are given by [1]:

and for light with perpendicular polarization,
 .
.
In these equations  ,
,  , and
, and  refer to the electric fields of the transmitted, reflected, and incident light beams.
refer to the electric fields of the transmitted, reflected, and incident light beams.  and
and  are the refractive indices of the first and second media. The angle of the transmitted beam
are the refractive indices of the first and second media. The angle of the transmitted beam  is related to the angle of incidence
is related to the angle of incidence  by Snell's law:
by Snell's law:
 .
.
In general, these electric field ratios are complex numbers and the transmission and reflection coefficients displayed here are the absolute values of these ratios:
 ,
,  ,
,  ,
, 
with the respective dephasings:
 ,
,  ,
,  ,
,  .
.
You obtain the power reflection coefficients by squaring the electric field ratios:
 ,
,  .
.
For the power transmission coefficients, a factor  is needed to account for the change of medium and a factor
is needed to account for the change of medium and a factor  for the change of surface area related to the change of direction of the transmitted beam. Therefore, you obtain:
for the change of surface area related to the change of direction of the transmitted beam. Therefore, you obtain:
 ,
,  .
.
You can check that they satisfy energy conservation:
 and
and  .
.
Note that in the case of total internal reflection, the transmitted electric field amplitude is different from zero, but it corresponds to an evanescent wave (not a traveling wave) and as a consequence the transmitted intensity and power are both equal to zero.
Reference:
[1] E. Hecht, Optics, 4th ed., Reading, MA: Addison–Wesley, 2002.
Permanent Citation