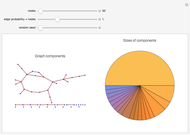
Giant Component in Random Graph

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
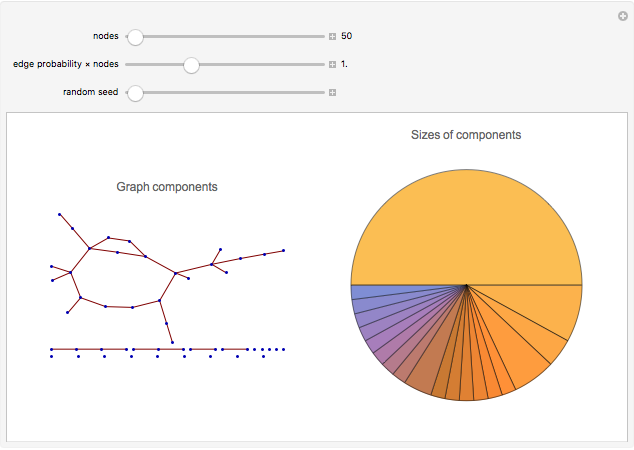
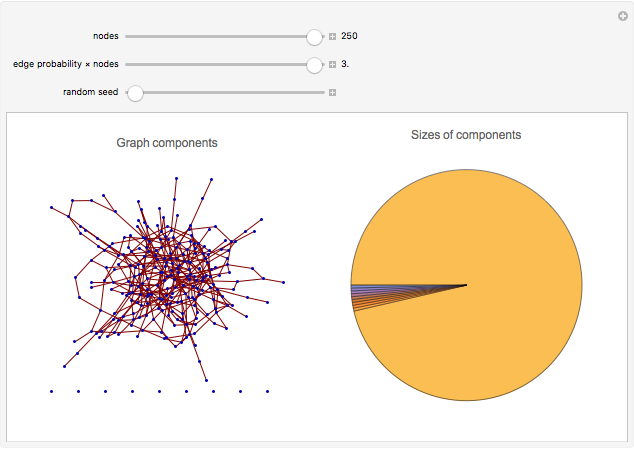
A random graph  is a graph with
is a graph with  nodes where the probability of finding an edge between two nodes is
nodes where the probability of finding an edge between two nodes is  . When
. When  tends to a constant
tends to a constant  (as
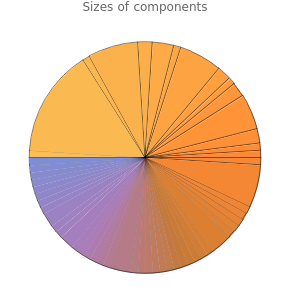
(as  grows), the graph will almost surely contain a "giant" connected component, absorbing a considerably large fraction of the nodes. This phenomenon is often mentioned as an example of emergence in random graph behavior.
grows), the graph will almost surely contain a "giant" connected component, absorbing a considerably large fraction of the nodes. This phenomenon is often mentioned as an example of emergence in random graph behavior.
Contributed by: Tommaso Bolognesi (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The emergence of a giant connected component plays a crucial role in the theory of autocatalytic chemical networks, which attempts to explain the appearance of life in the universe ("abiogenesis") as a self-organization phenomenon occurring within chemical systems. The idea was first proposed by Stuart Kauffman in 1995.
See the actual graph growth process at Giant Component.
S. Kauffman, At Home in the Universe: The Search for the Laws of Self-Organization and Complexity, Oxford: Oxford Univ. Press, 1995.
Permanent Citation
"Giant Component in Random Graph"
http://demonstrations.wolfram.com/GiantComponentInRandomGraph/
Wolfram Demonstrations Project
Published: March 7 2011