Global Minimum of a Non-Convex Function

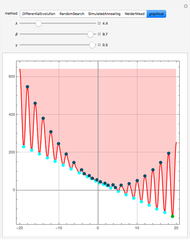
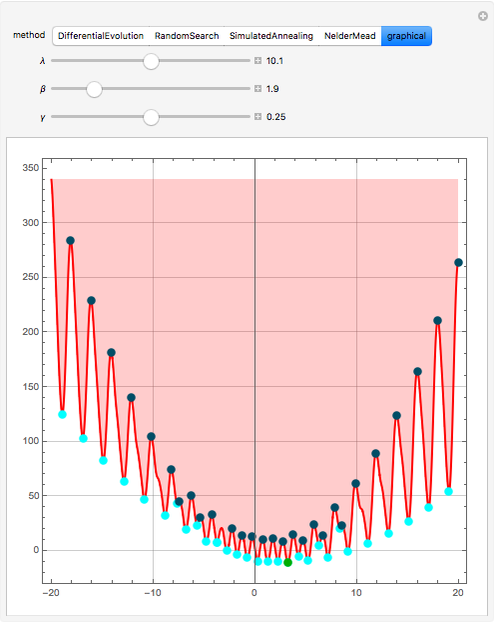
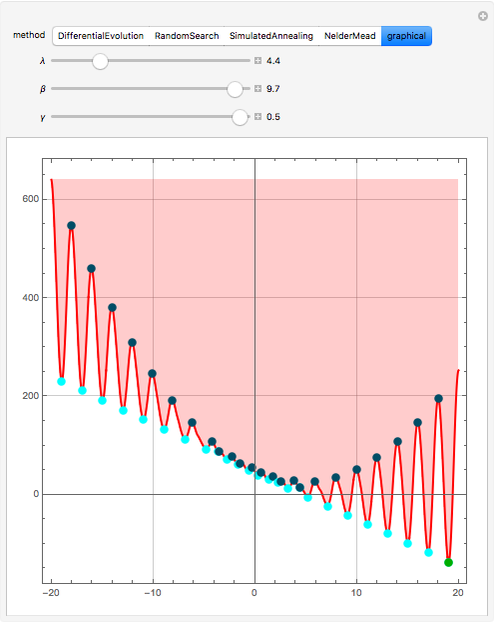
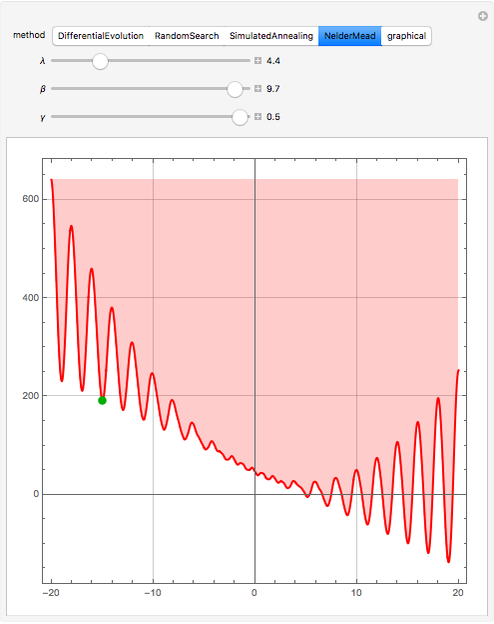
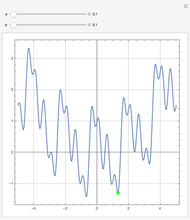
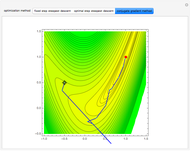
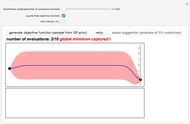
Consider the function family , which depends on three parameters—, , and —that you can vary. For the specified domain , has many local minima, the locations of which depend on the parameters. Because is nonlinear there is no guarantee that Mathematica's built-in function NMinimize will find a global minimum for a given set of its arguments. 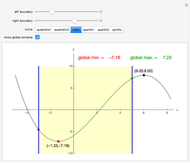This Demonstration determines the position of all the local minima and maxima as well as the global minimum of To do so, all roots of are computed using a graphical method developed by Wagon [1]. When , local minima occur at (cyan dots) and local maxima at (the dark blue dots). The green dot indicates the position of the purported global minimum. Finally, the result obtained using the built-in Mathematica function NMinimize is given for comparison. You can select from four of the methods used by NMinimize to assess a method's capability to find the global minimum of in the range .