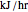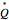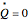Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Combustion Reactions in a Furnace

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

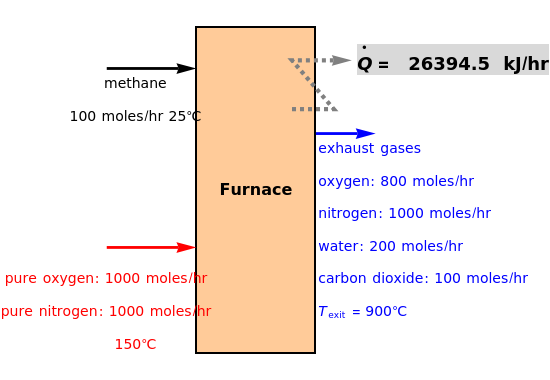
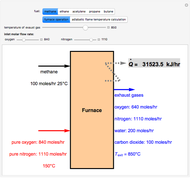
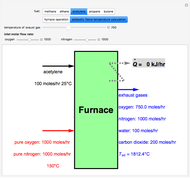
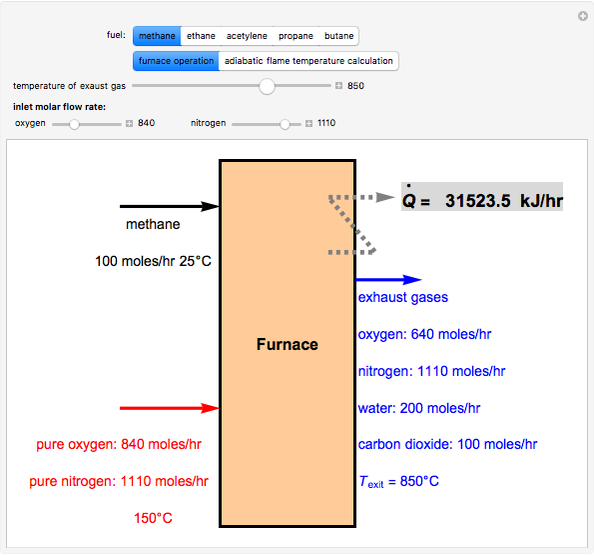
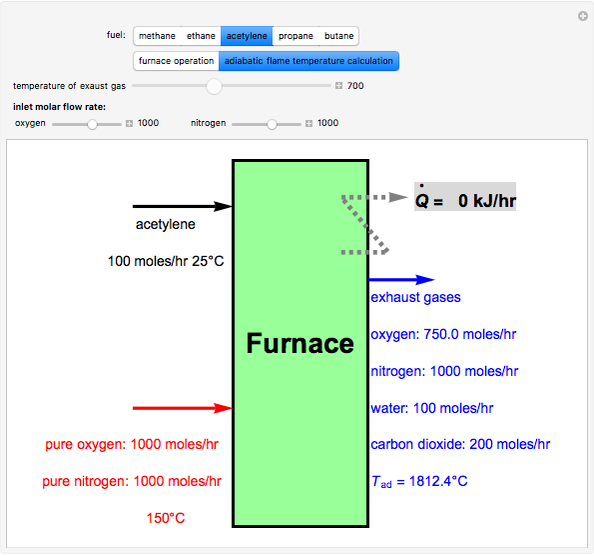
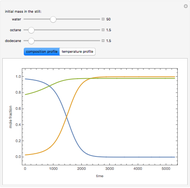
Fuel is fed to a furnace at 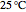and a molar flow rate of 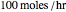. This fuel is one of these hydrocarbons: methane, ethane, acetylene, propane, or butane. The fuel is subject to a combustion reaction in the furnace: 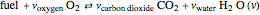, where 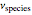is the stoichiometric coefficient of the chemical species. An excess of oxygen entering at 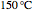is used for the combustion reaction, so that the conversion of the fuel is total. You can select the value of the inlet molar flow rate of oxygen and nitrogen. We apply the energy balance for reacting systems using the heat of reaction method [1]. The Demonstration determines:

[more]

1. the heat duty in (labeled in the process flowchart) for user-set values of exit temperature of the exhaust gases

or

2. the adiabatic flame temperature (i.e., for ) labeled in the process flowchart.

By specifying the exit temperature of the furnace, the enthalpy balance at steady operation requires that excess heat (denoted by ) from the exothermic reaction has to be removed. By specifying adiabatic operations, the heat released by the reaction raises the temperature of the exhaust gases. You can change the inlet molar flow rate of nitrogen and observe its effect on both on and .

[less]

Contributed by: Housam Binous, Ahmed Bellagi, and Brian G. Higgins (January 2015)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Reference

[1] R. M. Felder and R. W. Rousseau, Elementary Principles of Chemical Processes, 3rd ed., New York: John Wiley & Sons, 2004.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send