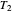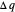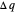Heat Transfer and the Second Law of Thermodynamics

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
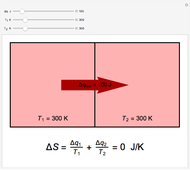
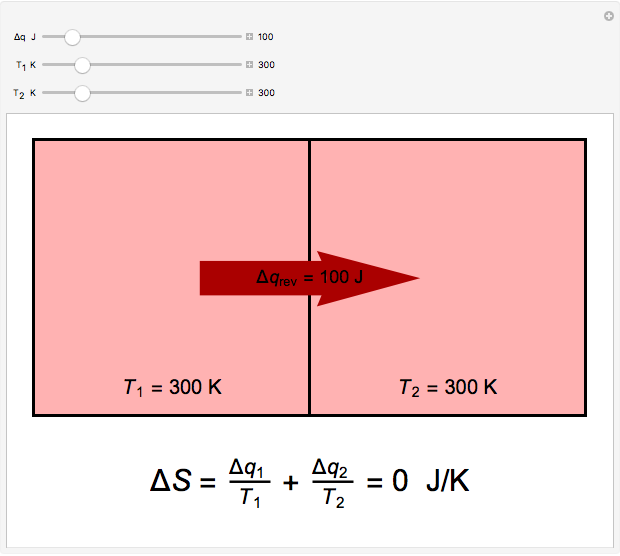
Two thermal reservoirs at the same temperature, 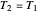 , can, in concept, exchange an increment of heat
, can, in concept, exchange an increment of heat 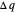 in either direction. Since it can just as easily flow in the opposite direction, this represents what is known as a reversible process and
in either direction. Since it can just as easily flow in the opposite direction, this represents what is known as a reversible process and  can be designated
can be designated  . By convention,
. By convention, 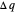 is positive if heat flows into a reservoir and negative (
is positive if heat flows into a reservoir and negative (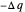 ) if it flows out. When
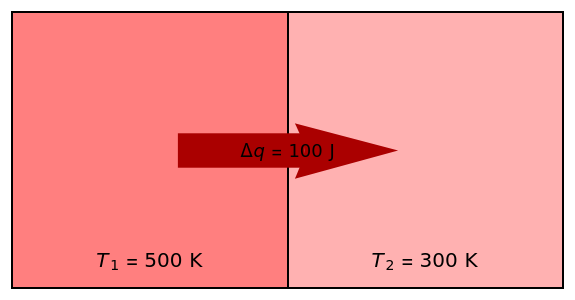
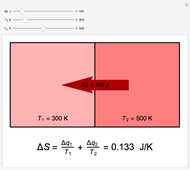
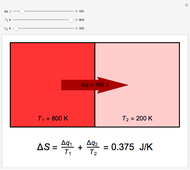
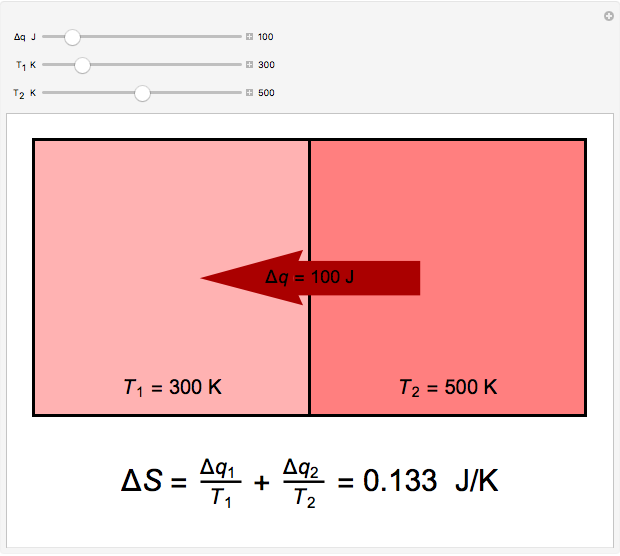
) if it flows out. When 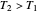 , it is a matter of experience that
, it is a matter of experience that  flows spontaneously (or irreversibly) from the hotter to the cooler reservoir. One can still set
flows spontaneously (or irreversibly) from the hotter to the cooler reservoir. One can still set 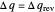 if one conceptualized an infinite number of intermediate reservoirs at temperature increments varying infinitesimally between
if one conceptualized an infinite number of intermediate reservoirs at temperature increments varying infinitesimally between  and
and  .
.
Contributed by: S. M. Blinder (April 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
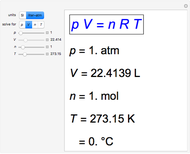
A differential statement of the first law of thermodynamics can be written  , where
, where  ,
,  , and
, and 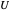 represent heat, work, and energy, respectively. Applied to a reversible process in an ideal gas, this can be specialized to
represent heat, work, and energy, respectively. Applied to a reversible process in an ideal gas, this can be specialized to  , where
, where  is the heat capacity at constant volume (equal to
is the heat capacity at constant volume (equal to 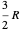 per mole for a monatomic ideal gas). Using the ideal gas law for 1 mole,
per mole for a monatomic ideal gas). Using the ideal gas law for 1 mole, 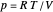 , we can write
, we can write 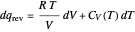 , which is not an exact differential—showing that
, which is not an exact differential—showing that  is not a function of state. Clearly, however,
is not a function of state. Clearly, however,  is an integrating factor for this expression, giving
is an integrating factor for this expression, giving  . This introduces a new function of state with
. This introduces a new function of state with 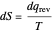 , where
, where  is called the entropy. This turns out to be a general result applicable to all thermodynamic systems.
is called the entropy. This turns out to be a general result applicable to all thermodynamic systems.
See any textbook on physical chemistry and many on general chemistry.
Permanent Citation