Ice Cube Melting in Water

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
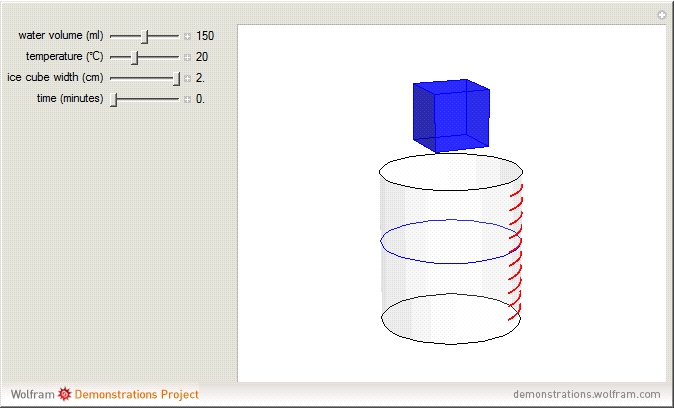
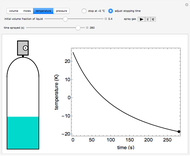
The rate at which an ice cube melts after being dropped into a beaker of water depends on the heat-transfer coefficient at an ice-water interface. (There are also some other variables not considered here.) However, values of this coefficient from various sources are not in very close agreement. We decided instead to do an experiment ourselves. We dropped an ice cube into a calibrated 250-ml beaker of tap water at a temperature of 15.0 °C. The initial water level of 175.0 ml rose to 194.5 ml and it took 7.515 minutes for the ice to melt. Once the ice becomes immersed in the water, the water level in the beaker remains at a constant level, even as the ice continues to melt. Remarkably, this provides sufficient data for all the necessary computations in this Demonstration, as described in the details section.
[more]
Contributed by: S. M. Blinder (August 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The density of ice at 0 °C is 0.917  ; the density of water is approximated as 1.000
; the density of water is approximated as 1.000  over the temperature range 0–60°C. Archimedes' principle states that a floating object displaces its own weight of water. Thus 91.7% of the cube lies beneath the surface. For the cube to lower its center of gravity, it reorients itself such that one of its three-fold axes is vertical. The remaining 8.3% forms a triangular pyramid of altitude
over the temperature range 0–60°C. Archimedes' principle states that a floating object displaces its own weight of water. Thus 91.7% of the cube lies beneath the surface. For the cube to lower its center of gravity, it reorients itself such that one of its three-fold axes is vertical. The remaining 8.3% forms a triangular pyramid of altitude  and volume
and volume  , with projecting surface area
, with projecting surface area  . Thus,
. Thus,  . (This is a nice exercise in solid geometry.)
. (This is a nice exercise in solid geometry.)
As a function of immersion time, the volume of the ice cube can be approximated by the differential equation  , where the constant is a lumped parameter depending on the ice/water interface heat transfer rate (e.g., in joules per unit area per unit time), the heat of fusion of ice, as well as the heat capacities of ice and water. Taking
, where the constant is a lumped parameter depending on the ice/water interface heat transfer rate (e.g., in joules per unit area per unit time), the heat of fusion of ice, as well as the heat capacities of ice and water. Taking  , the temperature
, the temperature  of the water in the beaker is
of the water in the beaker is  in °C, and is approximated to remain constant during the melting process. For a cube in the water,
in °C, and is approximated to remain constant during the melting process. For a cube in the water,  and
and  . Using the measurements obtained from our simple experiment, the instantaneous width of the ice cube (initially
. Using the measurements obtained from our simple experiment, the instantaneous width of the ice cube (initially  ) is approximated by
) is approximated by  , with
, with  in cm and
in cm and  in minutes.
in minutes.
It is assumed for simplicity that the ice maintains its cubic shape as it shrinks. Actually it deforms more irregularly and sometimes shows a beautiful fractal structure before it disappears.
Snapshot 1: beginning configuration
Snapshot 2: drop ice cube into water; note reorientation to lower center of gravity
Snapshot 3: ice cube begins to melt
Snapshot 4: melting completed
Snapshot 5: faster melting at higher water temperature
Snapshot 6: water at 0 °C; no net melting but dynamic equilibrium as ice and water exchange molecules
Reference
[1] Wikipedia. "Ice." (Aug 5, 2013) en.wikipedia.org/wiki/Ice
Permanent Citation