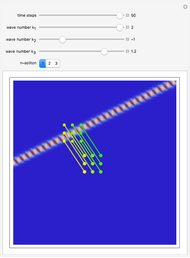
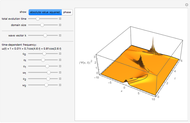
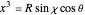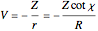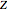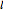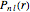Hydrogen Atom in Curved Space

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
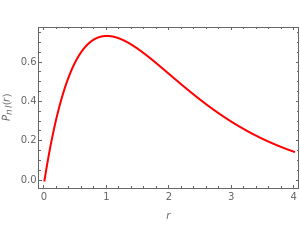
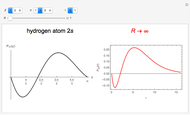
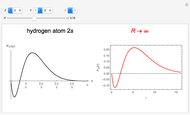
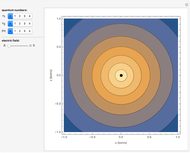
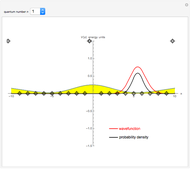
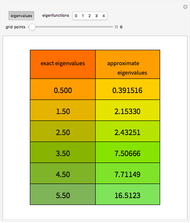
In 1940, Schrödinger considered the hypothetical problem of a hydrogen atom in a space of positive curvature [1, 2]. The actual curvature of space is far too feeble to have any detectable physical effect on an atomic scale, but this might become relevant in the neighborhood of a black hole or neutron star. Schrödinger was able to derive an exact solution with a remarkably simple energy spectrum:
[more]
Contributed by: S. M. Blinder (May 2018)
Open content licensed under CC BY-NC-SA
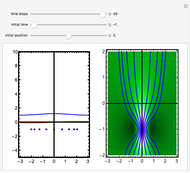
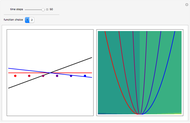
Snapshots
Details
The canonical partition function for the hydrogen atom had long presented a paradox since the summation over just the bound states
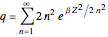
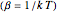
is divergent. However, by using the curved-space energies
 ,
,
a finite result can be derived [3], with the radius of curvature of the four-dimensional hypersphere serving as a "metaphor" for the volume in three-dimensional space, with the correspondence
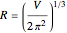 .
.
References
[1] E. Schrödinger, "A Method of Determining Quantum-Mechanical Eigenvalues and Eigenfunctions," Proceedings of the Royal Irish Academy. Section A: Mathematical and Physicial Sciences, 46, 1940 pp. 9–16. www.jstor.org/stable/20490744.
[2] N. Bessis and G. Bessis, "Electronic Wavefunctions in a Space of Constant Curvature," Journal of Physics A: Mathematical General, 12(11), 1979 pp. 1991–1997.
[3] S. M. Blinder, "Canonical Partition Function for the Hydrogen Atom in Curved Space," Journal of Mathematical Chemistry, 19(1), 1996 pp. 43–46. doi:10.1007/BF01165129.
Permanent Citation