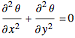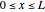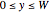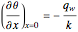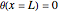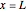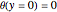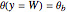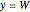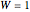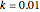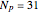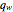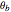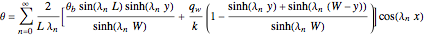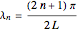Heat Transfer in a Bar with Rectangular Cross Section
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
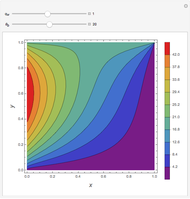
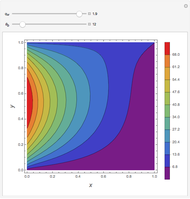
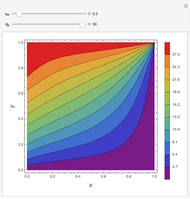
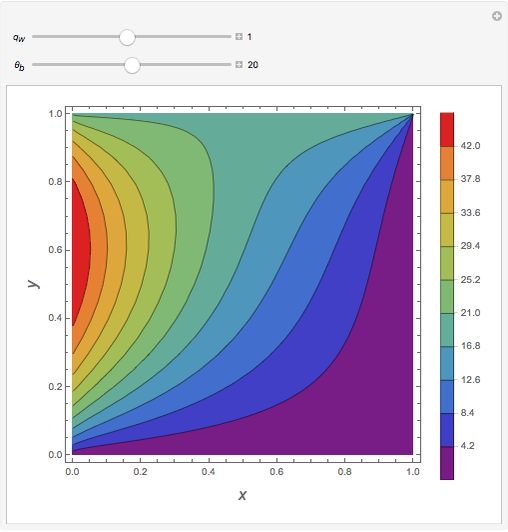
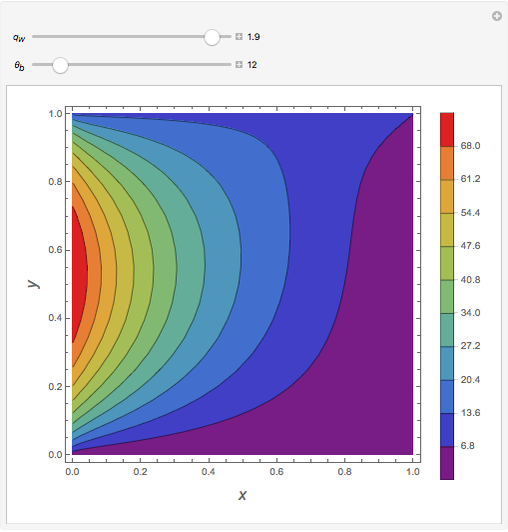
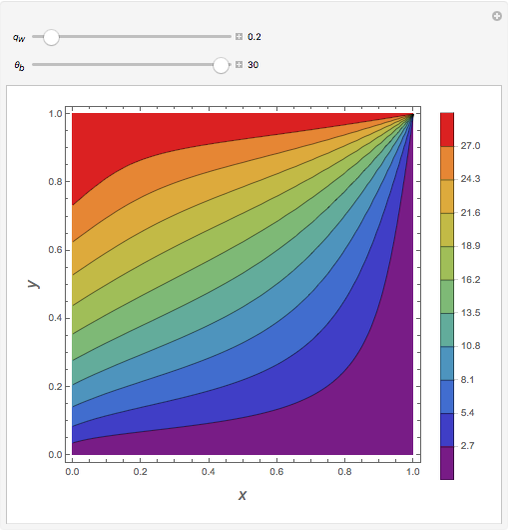
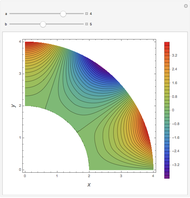
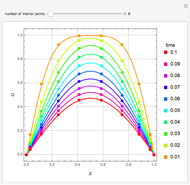
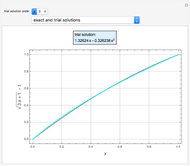
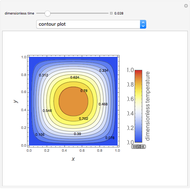
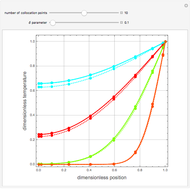
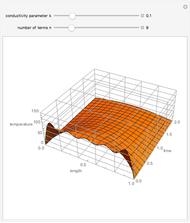
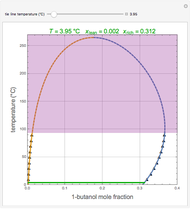
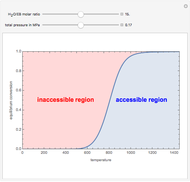
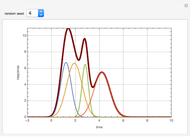
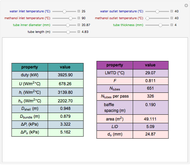
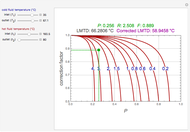
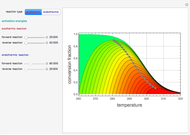
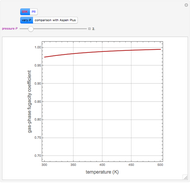
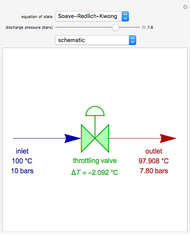
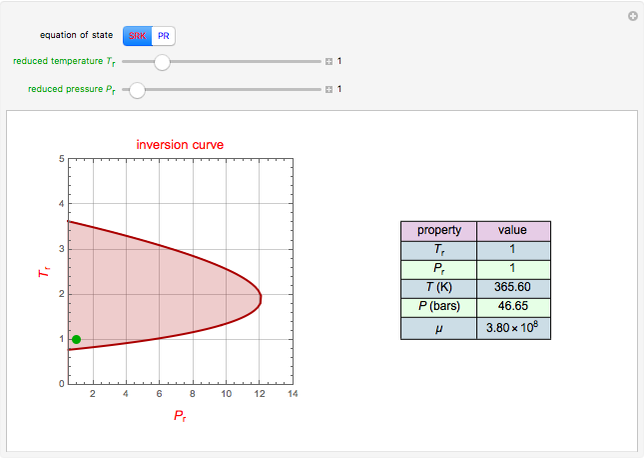
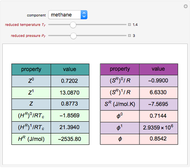
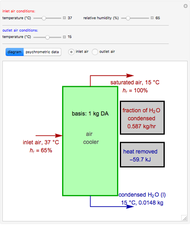
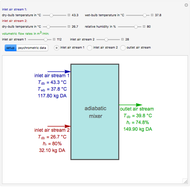
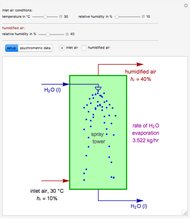
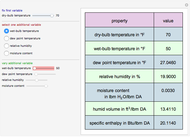
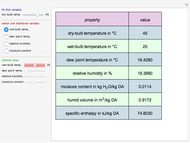
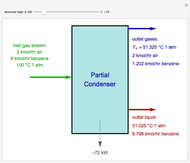
Consider a bar with a rectangular cross section subject to both temperature and heat flux boundary conditions.
[more]
Contributed by: Housam Binous and Ahmed Bellagi (August 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] T. Bennett, Transport by Advection and Diffusion, New York: Wiley, 2012.
Permanent Citation