Heat Transfer through a Cylinder

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
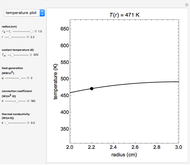
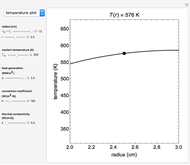
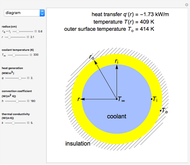
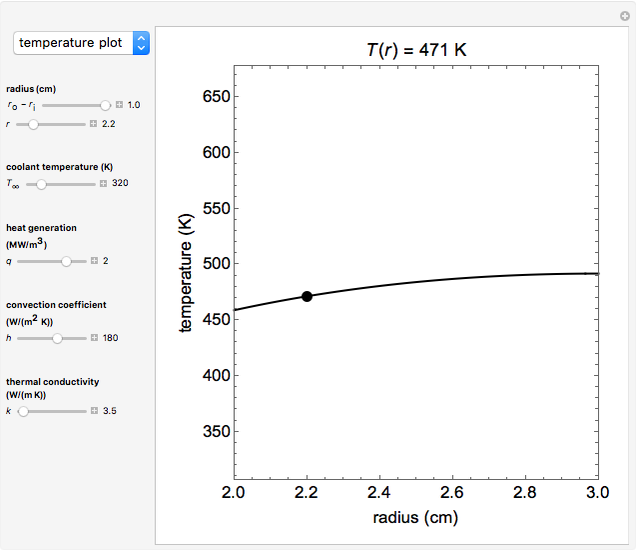
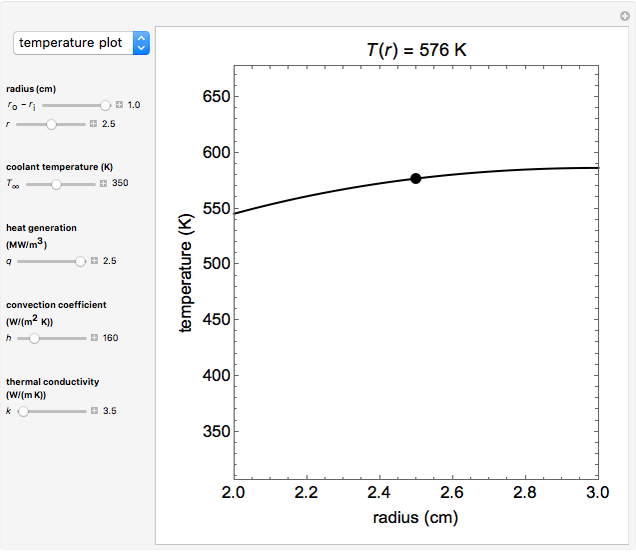
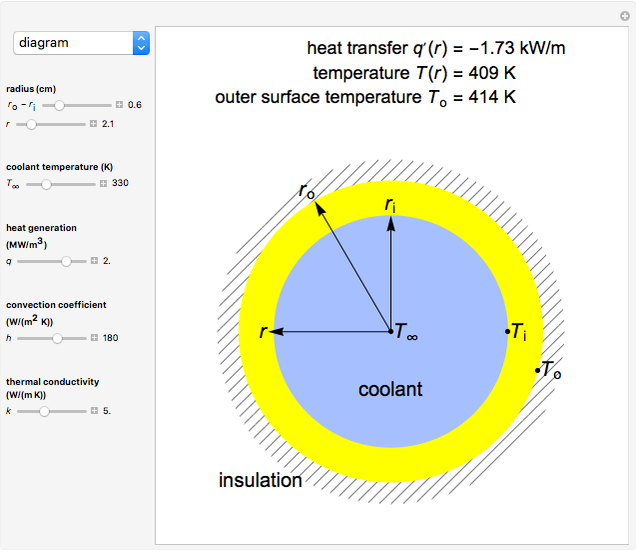
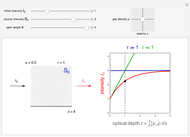
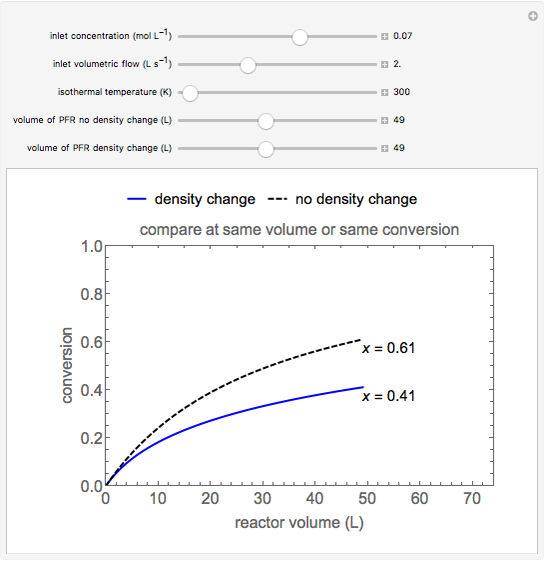
A long tube with a uniform heat source is insulated at its outer radius  and cooled at its inner radius
and cooled at its inner radius  , and the one-dimensional, radial, steady-state heat transfer is calculated. Use buttons to view a cross section of the tube or plot the temperature as a function of the radius. The heat transfer rate, temperature at position
, and the one-dimensional, radial, steady-state heat transfer is calculated. Use buttons to view a cross section of the tube or plot the temperature as a function of the radius. The heat transfer rate, temperature at position  and the outer surface temperature
and the outer surface temperature  are shown on the cross section diagram. Use sliders to set the coolant temperature, tube thickness
are shown on the cross section diagram. Use sliders to set the coolant temperature, tube thickness  , radial position, heat generation, convection coefficient and thermal conductivity.
, radial position, heat generation, convection coefficient and thermal conductivity.
Contributed by: Majed N. Aldossary and Rachael L. Baumann (February 2017)
Additional contributions by: John L. Falconer and Janet deGrazia
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For conduction through a cylinder with heat generation, the following assumptions are made:
1. steady-state conduction
2. one-dimensional radial conduction
3. constant thermodynamic properties
4. uniform volumetric heat generation
5. outer surface is adiabatic
The heat diffusion equation is solved to determine the radial temperature distribution  :
:
 .
.
The above assumptions reduce this equation to:
 .
.
Separating and integrating yields:
(1)  ,
,
(2)  .
.
Two boundary conditions are needed to determine constants  and
and  ; both conditions are evaluated at the outer radius
; both conditions are evaluated at the outer radius  :
:
(4)  ,
,
(5)  .
.
Evaluating equation (1) at boundary condition (5), evaluating equation (2) at boundary condition (4), and solving for  and
and  yields:
yields:
 ,
,
 .
.
The general solution for the temperature distribution is then:
 ,
,
where  is temperature,
is temperature,  is radius, the subscript
is radius, the subscript  refers to the outer surface,
refers to the outer surface,  is heat generation, and
is heat generation, and  is thermal conductivity.
is thermal conductivity.
From Fourier's law, the heat removal rate is:
 .
.
Substituting from  and evaluating at the inner radius
and evaluating at the inner radius  :
:
 .
.
Because the tube is insulated at  , the rate of heat generated in the tube must equal the rate of removal at
, the rate of heat generated in the tube must equal the rate of removal at  . Simplifying yields:
. Simplifying yields:
 .
.
The inner surface temperature  is calculated using the conservation of energy, since
is calculated using the conservation of energy, since  :
:
 ,
,
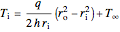 .
.
The outer surface temperature is found by evaluating  at
at  :
:
 ,
,
where  is the coolant temperature, and the subscript
is the coolant temperature, and the subscript  refers to the inner surface.
refers to the inner surface.
Reference
[1] T. L. Bergman, A. S. Lavine, F. P. Incropera and D. P. DeWitt, Fundamentals of Heat and Mass Transfer, 7th ed., Hoboken, NJ: John Wiley & Sons, 2011.
Permanent Citation