Heisenberg Uncertainty Product for Different Photon States

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
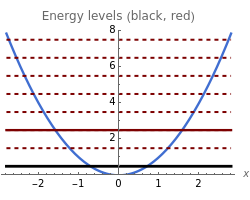
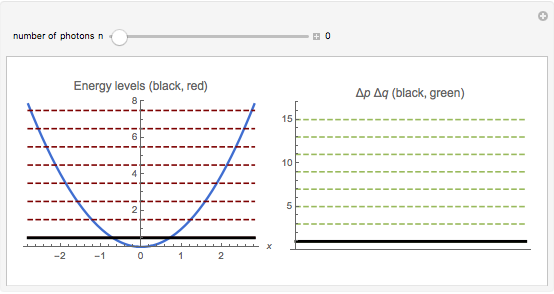
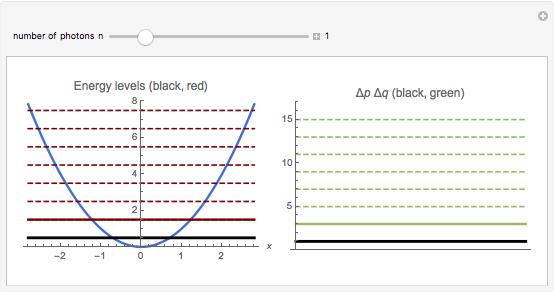
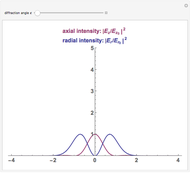
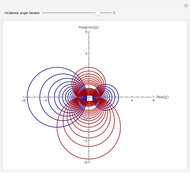
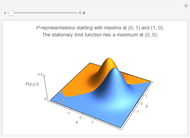
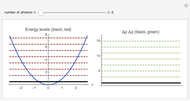
Each mode of the quantized radiation field can be associated with a quantized harmonic oscillator. This Demonstration shows the dependence of Heisenberg's uncertainty product (for momentum  and position
and position  ),
),  on the quantum number
on the quantum number  , when the oscillator has the energy eigenstate
, when the oscillator has the energy eigenstate  (in units of
(in units of  ). The integer
). The integer  denotes the energy and the number of photons in the radiation mode,
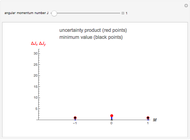
denotes the energy and the number of photons in the radiation mode,  . The uncertainty product is an increasing function of
. The uncertainty product is an increasing function of  . The minimal product
. The minimal product 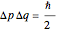 is valid for the energy ground state,
is valid for the energy ground state,  , represented by black lines in the diagrams.
, represented by black lines in the diagrams.
Contributed by: Reinhard Tiebel (March 2011)
Open content licensed under CC BY-NC-SA
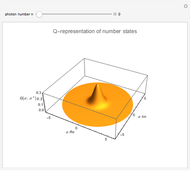
Snapshots
Details
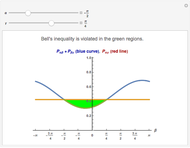
In quantum physics it is well known that two observables  and
and  can be incompatible, with
can be incompatible, with  . These are represented by noncommutating Hermitian operators:
. These are represented by noncommutating Hermitian operators:  . As a consequence, the uncertainties
. As a consequence, the uncertainties  and
and  do not vanish simultaneously;
do not vanish simultaneously;  denotes the variance of the operator
denotes the variance of the operator  . The variances depend on the actual state of the physical system. Therefore, no quantum state
. The variances depend on the actual state of the physical system. Therefore, no quantum state  exists for the physical system considered with
exists for the physical system considered with  and
and  . As an example, the Heisenberg uncertainty relation
. As an example, the Heisenberg uncertainty relation  follows from the quantum commutation relation of the noncommutating operators momentum
follows from the quantum commutation relation of the noncommutating operators momentum  and position
and position  and is valid for each quantum state.
and is valid for each quantum state.
References
[1] P. Meystre and M. Sargent III, Elements of Quantum Optics, New York: Springer–Verlag, 1991.
[2] M. O. Scully and M. S. Zubairy, Quantum Optics, Cambridge: Cambridge University Press, 1997.
[3] J. J. Sakurai, Modern Quantum Mechanics, Reading, MA: Addison–Wesley, 1995.
Permanent Citation