Transmission and Reflection Coefficients of Quantum Particles

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
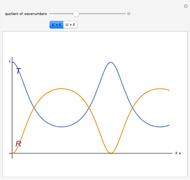
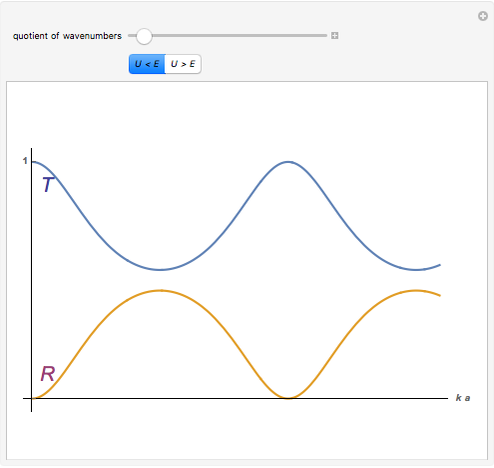
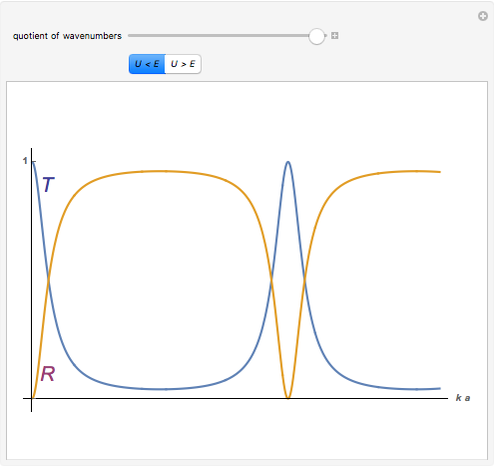
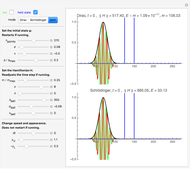
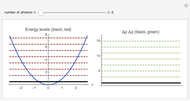
This Demonstration shows the transmission coefficient  and the reflection coefficient
and the reflection coefficient  of a quantum particle with energy
of a quantum particle with energy  hitting a rectangular potential barrier. See how the height of the potential barrier
hitting a rectangular potential barrier. See how the height of the potential barrier  affects
affects  and
and  by comparing the cases
by comparing the cases  and
and  . The dimensionless coordinate
. The dimensionless coordinate  is the product of the wavenumber
is the product of the wavenumber  for the wave inside the barrier and the barrier width
for the wave inside the barrier and the barrier width  .
.
Contributed by: Reinhard Tiebel (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
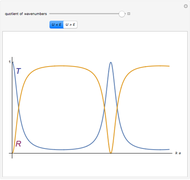
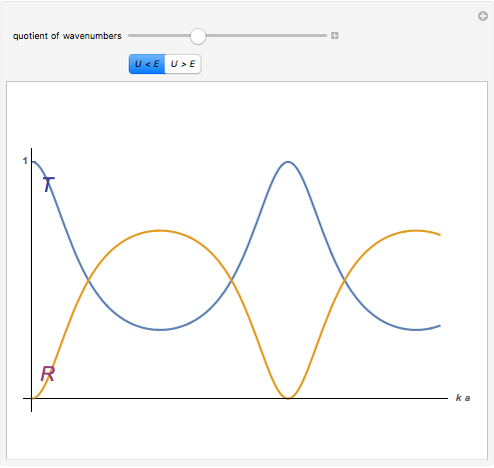
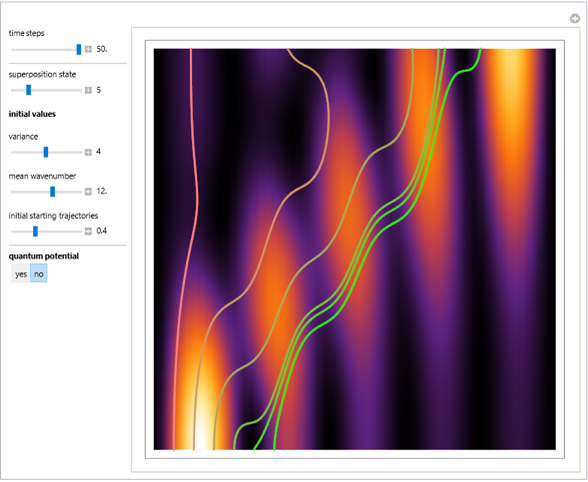
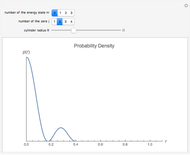
If a quantum particle hits a rectangular potential barrier, then both the transmission coefficient  and the reflection coefficient
and the reflection coefficient  are periodic functions of the potential width
are periodic functions of the potential width  in the case
in the case  , but
, but  and
and  are decreasing and increasing functions, respectively, in the case
are decreasing and increasing functions, respectively, in the case  . Furthermore,
. Furthermore,  and
and  depend on the quotient
depend on the quotient  of the wavenumbers
of the wavenumbers  of the incident particle and
of the incident particle and  of the wave inside the barrier;
of the wave inside the barrier;  . This is shown interactively. The behavior of a quantum particle contrasts with that of a classical particle, where
. This is shown interactively. The behavior of a quantum particle contrasts with that of a classical particle, where  ,
,  , or vice versa. The "quantum tunneling" effect is a pure quantum effect in the case
, or vice versa. The "quantum tunneling" effect is a pure quantum effect in the case  . The formulas for
. The formulas for  and
and  follow by solving the time-independent wave equation (Schrödingers equation) with boundary conditions.
follow by solving the time-independent wave equation (Schrödingers equation) with boundary conditions.
Permanent Citation