Energy Levels in a Half-Infinite Linear Well

Initializing live version

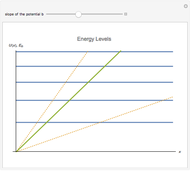
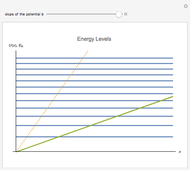
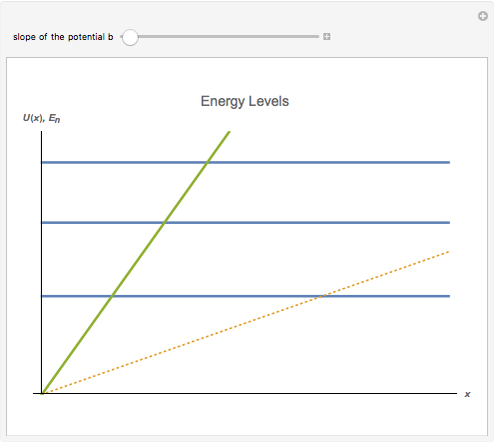
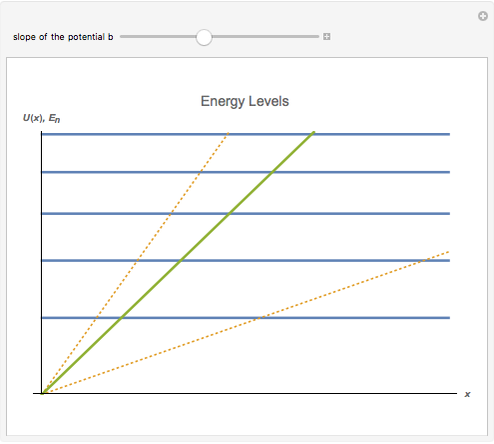
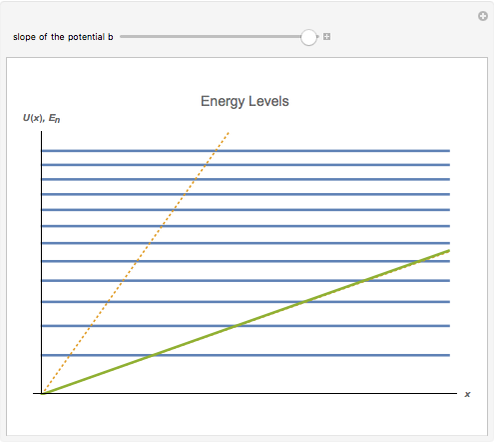
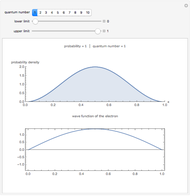
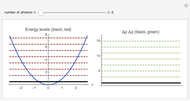
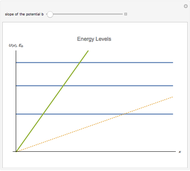
The energy spectrum of a quantum particle moving in a potential well is discrete. The density of energy eigenstates grows as the potential well's slope decreases. This is similar to the behavior of a free particle.

Contributed by: Reinhard Tiebel (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

A wall of infinite height at the origin makes value of

inaccessible to the particle.

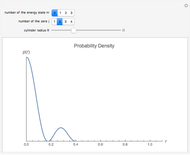
The

lowest twelve energy values are calculated numerically. The number of the energy levels

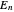
is infinite; they can be calculated from solutions of the

eigenvalue problem of the Hamiltonian (these are solutions of the stationary Schrödinger equation):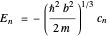

where

is the reduced Planck's constant (

is the mass of the atom,

is the slope of the linear potential

, and

(

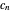
= 1, 2, ...) are

the zeros of the Airy function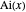

. All of these lie on the negative part of the

axis.

Permanent Citation

Reinhard Tiebel "Energy Levels in a Half-Infinite Linear Well"
http://demonstrations.wolfram.com/EnergyLevelsInAHalfInfiniteLinearWell/
Wolfram Demonstrations Project
Published: March 7 2011


Feedback (field required)

Email (field required)	Name

Occupation	Organization

Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback. Send