Hippias Quadratrix

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
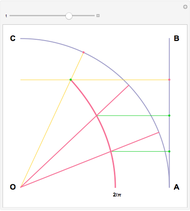
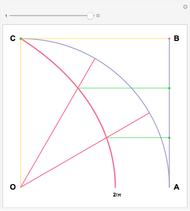
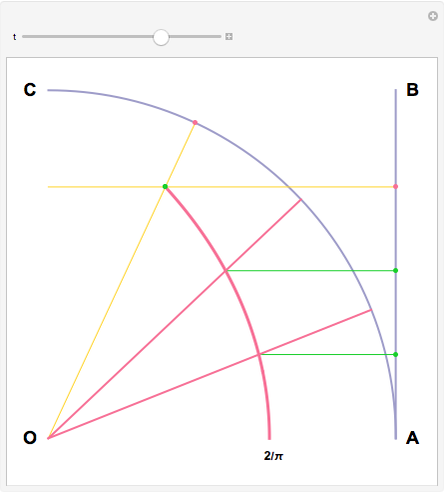
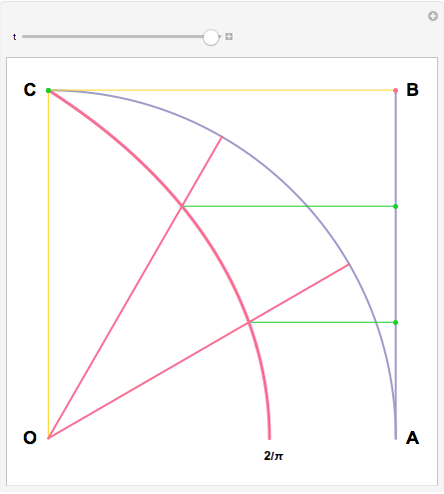
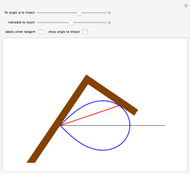
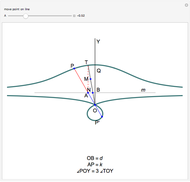
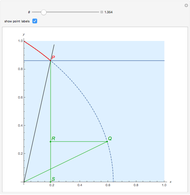
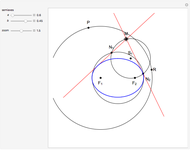
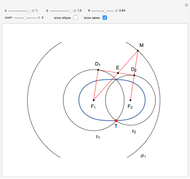
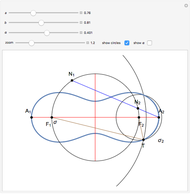
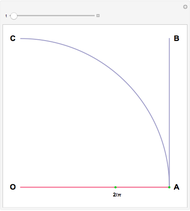
Hippias lived in the time of Socrates and was one of the great Sophists. He was a smart and unconventional character who did not accept the preeminence of ruler and compass in geometry. The quadratrix that he proposed solves the problem of trisecting an angle. Two "flies" start from A and fly at constant speed. One goes to B on a straight line, the other to C on the arc. They arrive at their destination at the same time. The quadratrix is obtained by intersecting the yellow lines. The segment which joins A to the first fly is cut into three equal parts. The angle formed by OA and the yellow radius is trisected by joining O to the intersections of the green segments with the quadratrix.
Contributed by: Bruno Autin (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Hippias Quadratrix"
http://demonstrations.wolfram.com/HippiasQuadratrix/
Wolfram Demonstrations Project
Published: March 7 2011