Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

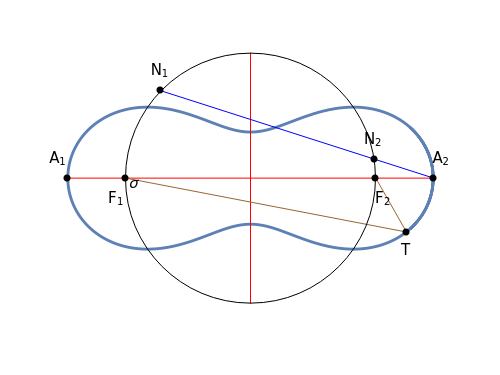
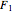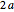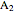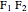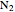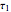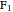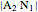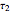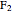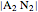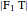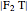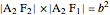1. Constructing a Point on a Cassini Oval

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

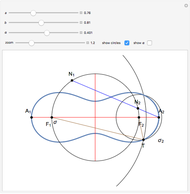
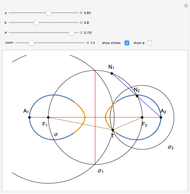
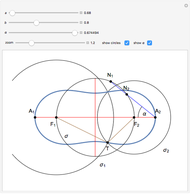
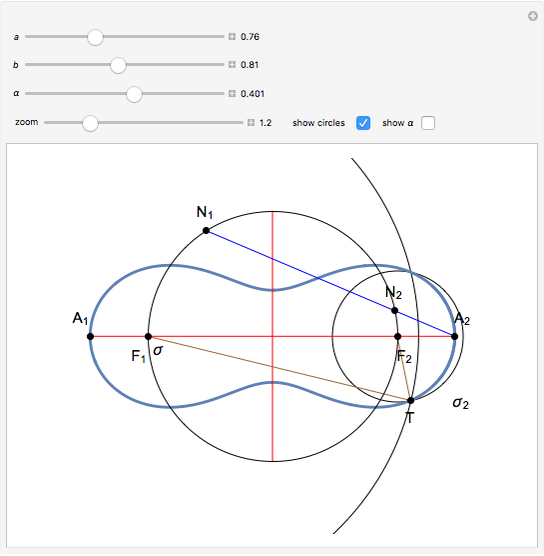
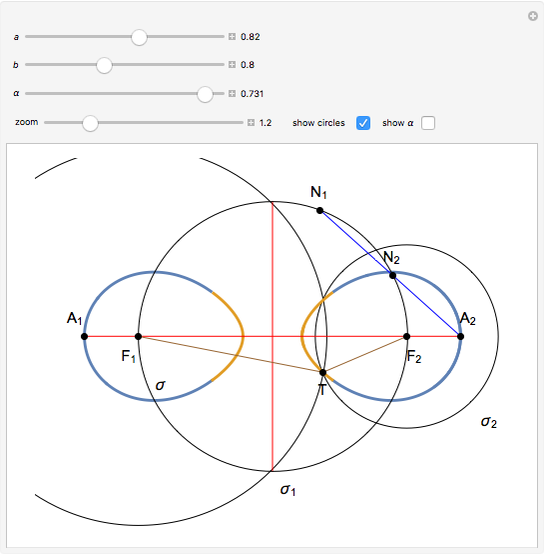
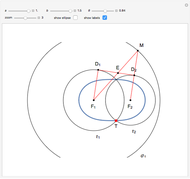
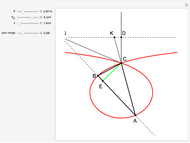
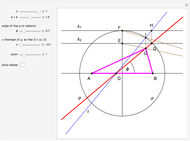
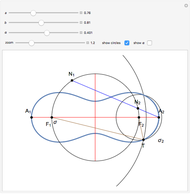
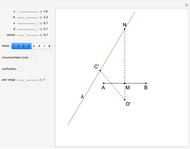
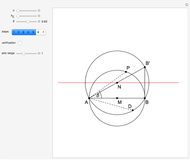
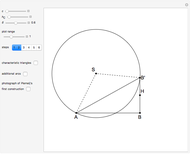
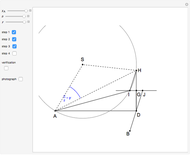
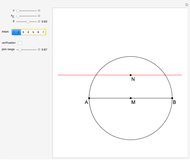
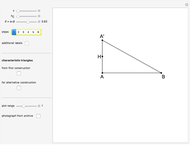
This Demonstration shows a ruler and compass construction of a point on a Cassini oval.

[more]

Fix two points, and (the foci), a distance apart. A Cassini oval (or Cassini ellipse) is a quartic curve traced by a point such that the product of the distances is a constant .

Let be the circle with center at the center of the oval and radius . Let be the right apex of the oval. A ray from at an angle to the line meets at the points and . Let be the circle with center and radius and let be the circle with center and radius . Let the point be one of the intersections of and . Then the product of the radii and is equal to the product , so is on the oval.

[less]

Contributed by: Izidor Hafner and Marko Razpet (March 2018)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The construction can be found in [2, pp. 189–190].

References

[1] E. W. Weisstein. "Cassini Ovals" from Wolfram MathWorld—A Wolfram Web Resource. mathworld.wolfram.com/CassiniOvals.html (Wolfram MathWorld).

[2] A. A. Savelov, Plane Curves (in Croatian), Zagreb: Školska knjiga, 1979.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send