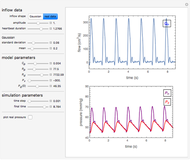
Hodgkin-Huxley Action Potential Model

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
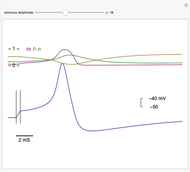
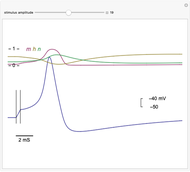
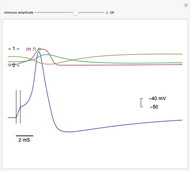
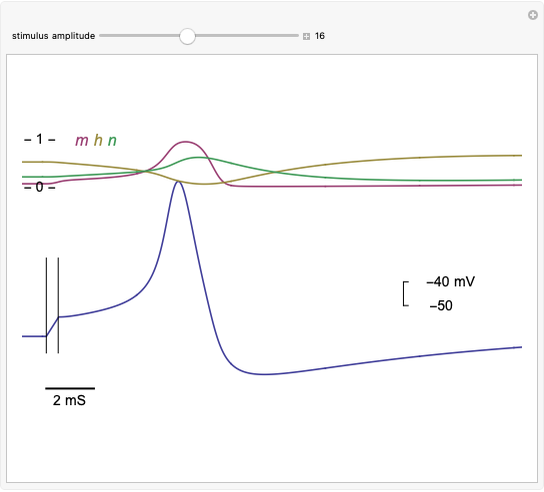
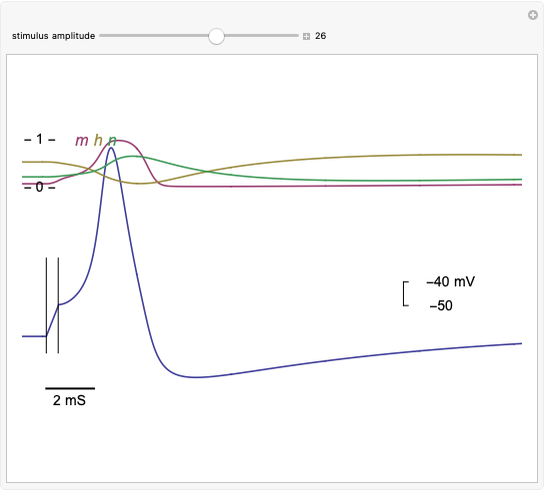
The voltage across membranes of excitable cells (e.g. nervous system, muscles, heart, endocrine system) transiently changes, creating a pulse-like wave called an "action potential". The action potential serves as a major signal for the initiation of many cellular and intercellular processes. The canonical mathematical-physical model of the phenomenon was presented by Alan Hodgkin and Andrew Huxley in 1952 in a series of seminal papers [2], where membrane potential dynamics is described in terms of voltage-dependent ionic conductance, dominated by four coupled ordinary differential equations. In the Demonstration presented here, the action potential is triggered by a short current stimulus. Shown are time evolutions of membrane voltage (blue trace) and conductance gates (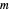 ,
,  , and
, and 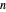 ).
).
Contributed by: Shimon Marom (April 2012)
Open content licensed under CC BY-NC-SA
Details
Units: 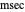 ,
, 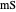 ,
, 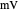 , and
, and 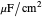 .
.
Rate functions:
αm=0.1 (v+40)/(1-exp(-0.1(v+40))); βm=4 exp(-0.05(v+65)); αn=-0.01(v+55)/((exp(-0.1(v+55))-1); βn =0.25 exp(-0.0125(v+65)); αh=0.07 exp(-0.05(v+65)); βh =1/((exp(-0.1(v+55))+1)
Parameters:
Maximal conductances are 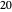 ,
, 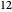 , and
, and  for sodium, potassium, and leak, respectively. Nernst equilibrium potentials are
for sodium, potassium, and leak, respectively. Nernst equilibrium potentials are 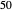 ,
,  , and
, and 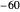 for sodium, potassium, and leak, respectively. Membrane capacitance is set to 1.
for sodium, potassium, and leak, respectively. Membrane capacitance is set to 1.
References
[1] B. Hille, Ion Channels of Excitable Membranes, Sunderland, MA: Sinauer, 2001.
[2] A. L. Hodgkin and A. F. Huxley, "A Quantitative Description of Membrane Current and Its Application to Conduction and Excitation in Nerve," Journal of Physiology, 117, 1952 pp. 500–544.
Snapshots
Permanent Citation