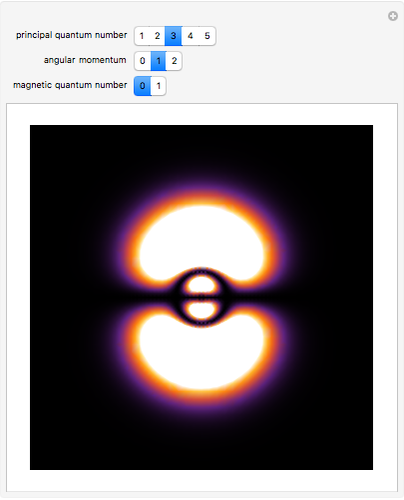
Hydrogen Atom: Fine Structure of Energy Levels

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
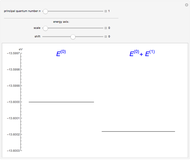
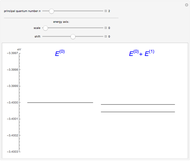
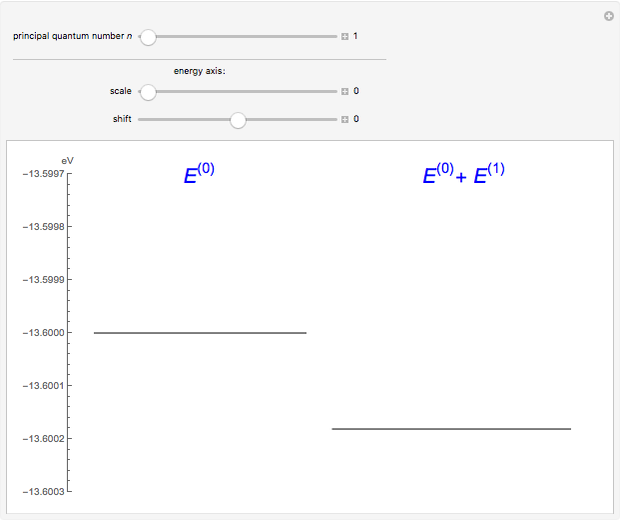
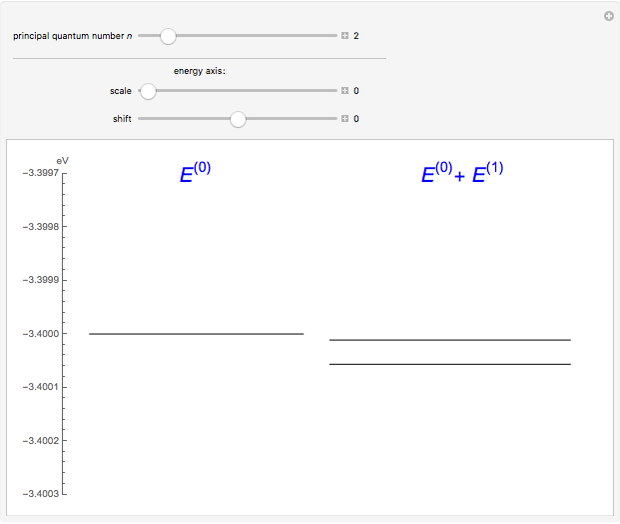
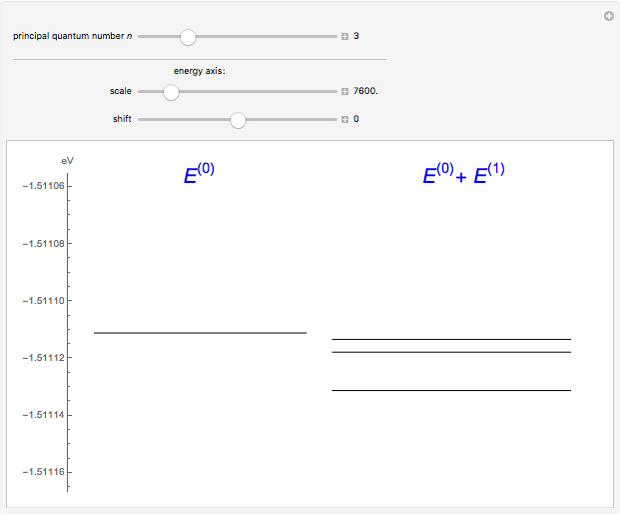
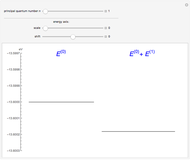
The energy levels of the hydrogen atom 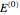 , taking account only of the Coulomb interaction between the electron and proton, are shown on the left. Perturbed energy levels
, taking account only of the Coulomb interaction between the electron and proton, are shown on the left. Perturbed energy levels  , also including spin-orbit interaction and relativistic corrections, produce the so-called fine structure, as shown on the right.
, also including spin-orbit interaction and relativistic corrections, produce the so-called fine structure, as shown on the right.
Contributed by: Lukás Rafaj (May 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Atomic structure, specifically for the hydrogen atom, is determined principally by Coulomb interactions among electrons and the nucleus. This leads to the unperturbed energy 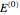 . There also exist smaller contributions to the energy, most notably from spin-orbit interactions. These are interactions between orbital and spin magnetic moments of the electron, represented by the Hamiltonian
. There also exist smaller contributions to the energy, most notably from spin-orbit interactions. These are interactions between orbital and spin magnetic moments of the electron, represented by the Hamiltonian
 ,
,
where  and
and  are the orbital and spin angular momenta, respectively. A secondary perturbation comes from relativistic corrections to electron kinetic energy, represented by a term in the Hamiltonian of the form
are the orbital and spin angular momenta, respectively. A secondary perturbation comes from relativistic corrections to electron kinetic energy, represented by a term in the Hamiltonian of the form
 .
.
The total fine structure is then represented by the perturbation
 ,
,
with a first-order energy correction
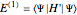 .
.
This gives the total energy of the state  ,
,  , to first order in perturbation theory,
, to first order in perturbation theory,
 ,
,
where  is the principal quantum number,
is the principal quantum number,  is the total electronic angular momentum quantum number and
is the total electronic angular momentum quantum number and  is the fine-structure constant
is the fine-structure constant  .
.
Permanent Citation