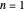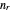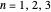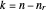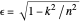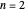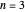Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

The Fine-Structure Constant from the Old Quantum Theory

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

The fine structure constant, 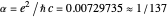, measures the relative strength of the electromagnetic coupling constant in quantum field theory. Its small magnitude enables very accurate predictions in the perturbation expansions of quantum electrodynamics. This famous dimensionless parameter was first introduced by Arnold Sommerfeld in 1916 in a relativistic generalization of Bohr's atomic theory. As its simplest physical realization, the fine structure constant is equal to the ratio of the speed of the electron in the first Bohr orbit to the speed of light.

[more]

In Sommerfeld's first modification of the original atomic theory, the circular Bohr orbits were generalized so that elliptical orbits could also occur, in analogy with Kepler's laws of planetary motion. Bohr energy levels above the ground state were thereby shown to be degenerate, involving two quantum numbers, and . Sommerfeld later used the relativistic kinetic energy formula to introduce corrections to the electronic orbits. This caused some of the degenerate levels to split, thereby accounting for the "fine structure" of atomic spectral lines. Classically, the perturbation causes the relativistic elliptical orbits to precess about their major axes, although slowly compared to the electron's orbital speed.

The more general significance of the fine structure constant emerged only several years after Sommerfeld introduced it. Eddington promoted the integer approximating its reciprocal (136, and later 137, as measurements became more accurate) to a near-mystical quantity, which he claimed was central to the structure of the entire universe. Pauli, for many years, sought its origin from some deeper physical principle. Today we understand that the Standard Model (SM) contains some 20 or so coupling constants, masses and mixing angles, including the fine-structure constant, which can only be experimentally determined. It is hoped that some future successor to the SM will come closer to predicting the values of these constants.

The graphics in this Demonstration show electron orbits for the principal quantum numbers , for both the nonrelativistic and relativistic theories. The quantum number determines the eccentricity via . Note that increasing corresponds to more circular orbits, in contrast to the more familiar angular-momentum quantum number , for which decreasing values give more circular orbits. The selected orbit is shown as a red curve, while the other orbits are lighter curves. For clarity, the and orbits are shown simultaneously, while the orbits are in a separate graphic. The precessional rates are exaggerated for purposes of visualization.

[less]

Contributed by: S. M. Blinder (March 2012)
Open content licensed under CC BY-NC-SA

Snapshots

Details

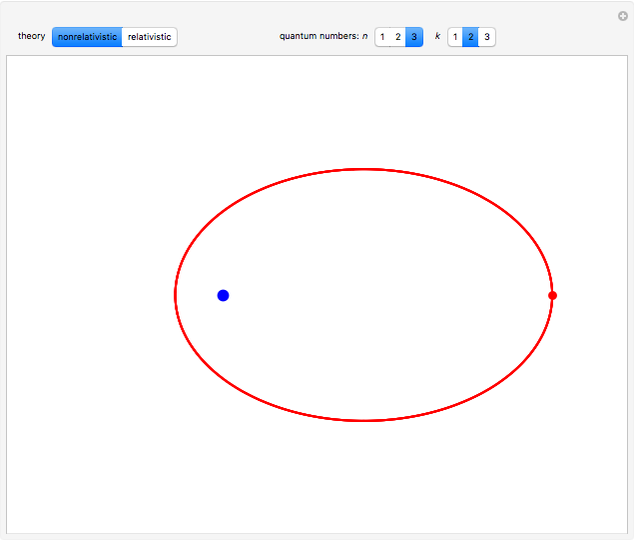
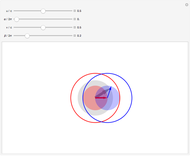
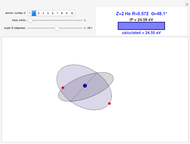
The nonrelativistic version of the old quantum theory was most succinctly expressed by the Sommerfeld–Wilson quantum conditions: 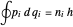, for each periodic degree of freedom in the system. For example, the Keplerian orbital motion of a bound state of the electron in a hydrogen atom, an ellipse confined to a plane, has two degrees of freedom. 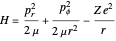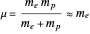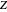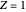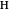The Hamiltonian can be written , where is the reduced mass and is the nuclear charge ( for , for 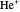, etc.). For simplicity, we use atomic units 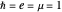and assume infinite nuclear mass. Thus the Bohr radius is 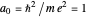. The two quantum conditions are the phase integrals 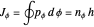and 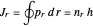. The first is simple, since the Hamiltonian is independent of , so that 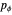is a constant. Thus 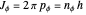or 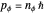, with 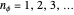. This represents, in fact, the quantization of angular momentum. The integral 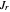is a bit more challenging: 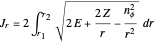, where 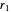and are the periapsis and apoapsis of the orbit. This works out to 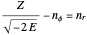, with 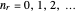. 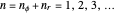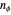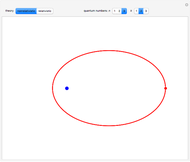The energy, in atomic units, reduces to the familiar Bohr formula , where the principal quantum number , and the azimuthal quantum number , usually written as , has the allowed values 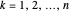. The elliptical orbits are given by the polar equations 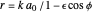, with the eccentricity .

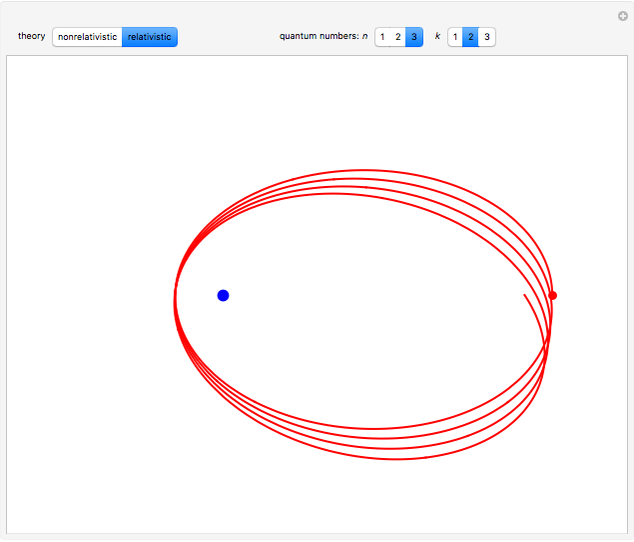
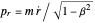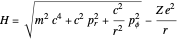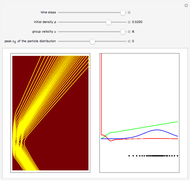
In the relativistic generalization of Sommerfeld's orbits, the radial and angular momenta of the electron are given by , , where . These contain essentially relativistic generalizations of the components of kinetic energy. The Hamiltonian takes the form . Evaluation of the phase integrals is more complicated, and the interested reader is directed to the references. The relativistic energy works out to 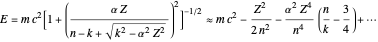. 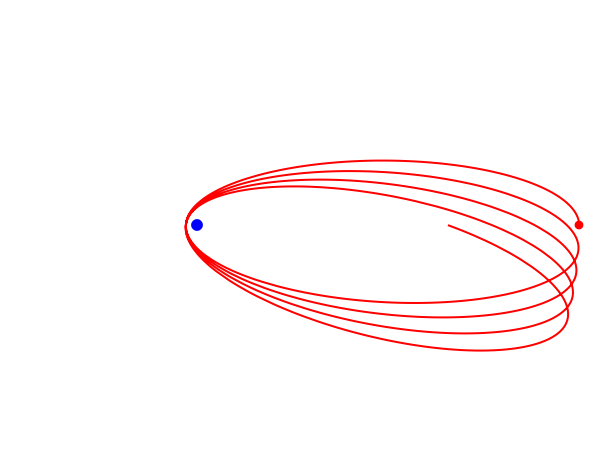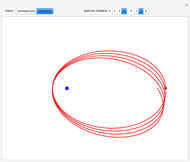The third term in the expansion represents the fine-structure splitting, which removes the degeneracy in for 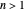. In the relativistic theory, the elliptical orbits precess about their major axes.

Remarkably, Sommerfeld's formula agrees exactly with the result obtained by solution of the Dirac equation for the hydrogen atom in relativistic quantum mechanics. To be blunt, this is really "dumb luck," since Sommerfeld was, at the time, unaware of electron spin, whereas the Dirac formula actually takes account of the electron's spin-orbit coupling. And, of course, the angular momenta in the old quantum theory are too large by one unit of ℏ.

References

[1] A. Sommerfeld, Atombau und Spektrallinien, 4th ed., Braunschweig, Germany: F. Vieweg & Sohn, 1924 pp. 504–521.

[2] L. Page, Introduction to Theoretical Physics, 3rd ed., Princeton: Van Nostrand, 1952 pp. 670–680.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send