American Capped Call Options with Constant Cap

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
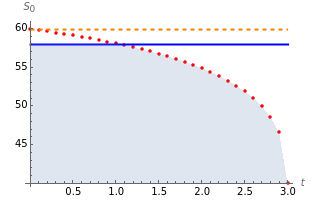
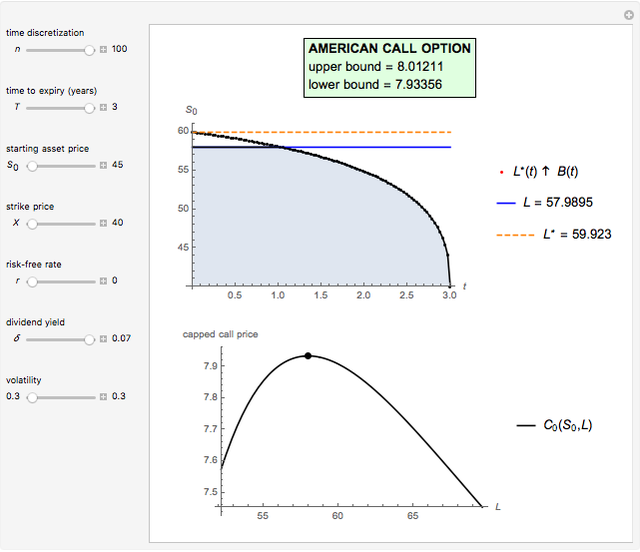
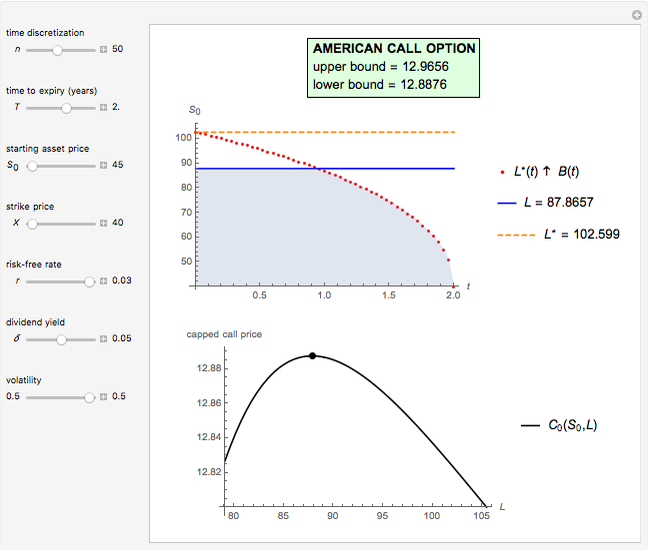
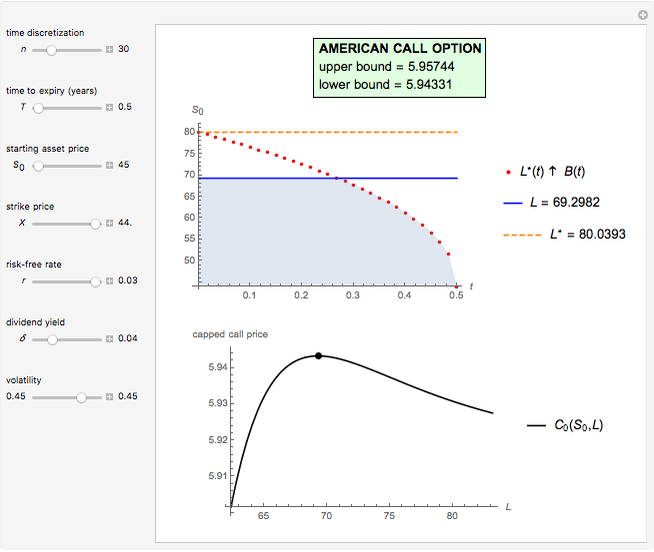
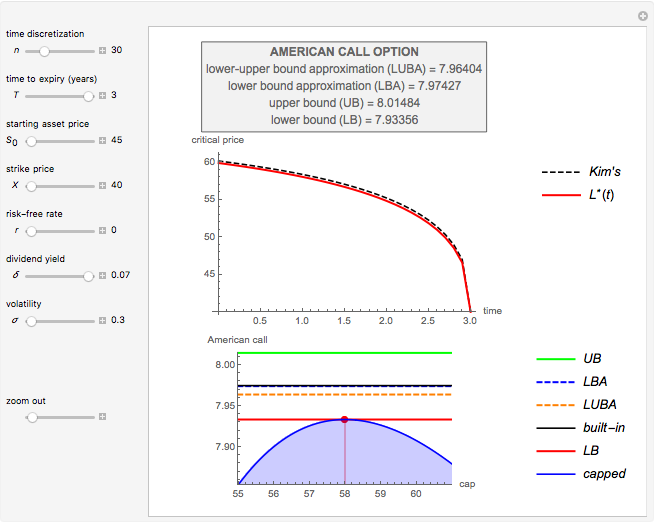
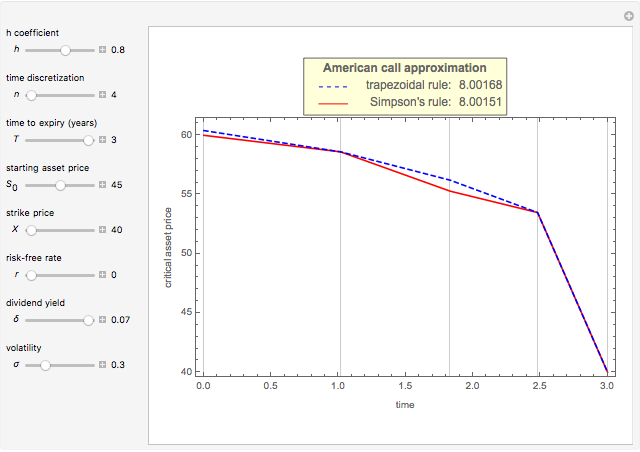
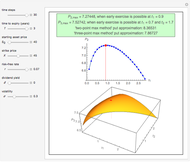
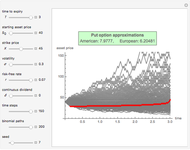
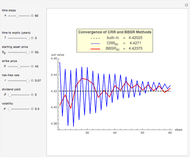
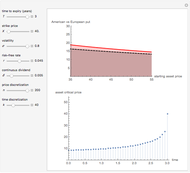
This Demonstration shows the maximization process of an American capped call option with a constant cap (or barrier). Because the capped call must be instantly exercised if the underlying asset price rises above a predetermined price 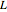 , which is called the "cap" or "cap price", its value never exceeds the value of the standard American call. Thus, identifying the cap
, which is called the "cap" or "cap price", its value never exceeds the value of the standard American call. Thus, identifying the cap 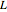 that maximizes the capped call payoff function
that maximizes the capped call payoff function 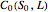 , we obtain a lower bound
, we obtain a lower bound 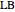 for the American call price. Moreover, the evaluation of the capped call payoff function derivative with respect to the cap, while the underlying asset price approaches the cap from below, provides a lower approach
for the American call price. Moreover, the evaluation of the capped call payoff function derivative with respect to the cap, while the underlying asset price approaches the cap from below, provides a lower approach 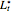 for the American call optimal exercise boundary
for the American call optimal exercise boundary 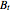 [1]. Finally, after replacing
[1]. Finally, after replacing 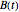 with
with 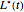 in Kim's integral equation [2], an upper bound
in Kim's integral equation [2], an upper bound 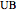 for the American call price is obtained. Thus the capped call option is really a tool used to bracket the pricing of the commonly traded American option.
for the American call price is obtained. Thus the capped call option is really a tool used to bracket the pricing of the commonly traded American option.
Contributed by: Michail Bozoudis (February 2016)
Suggested by: Michail Boutsikas
Open content licensed under CC BY-NC-SA
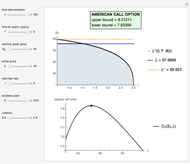
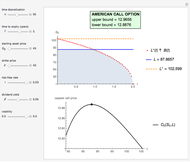
Snapshots
Details
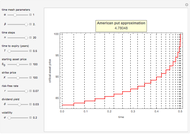
M. Broadie and J. Detemple [3] developed an analytical formula to estimate American capped call options. In order to approximate an American call payoff 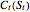 , they use the value of a capped call written on the same asset [1]. If the price of the underlying asset is
, they use the value of a capped call written on the same asset [1]. If the price of the underlying asset is 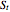 , when
, when 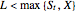 the payoff of a capped call option is
the payoff of a capped call option is 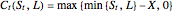 , where
, where 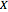 is the strike price and
is the strike price and 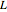 is the cap. The payoff is the same as a standard American option, except that the cap
is the cap. The payoff is the same as a standard American option, except that the cap 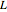 limits the maximum possible payoff. Since the policy of exercising when the asset price reaches the constant cap
limits the maximum possible payoff. Since the policy of exercising when the asset price reaches the constant cap 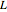 is an admissible policy for the American option,
is an admissible policy for the American option, 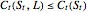 for any
for any 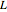 .
.
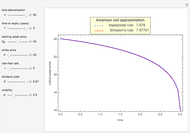
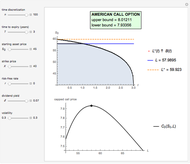
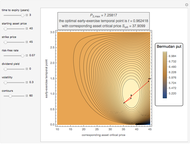
Hence a lower bound 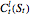 is still obtained after optimizing over
is still obtained after optimizing over 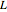 :
:
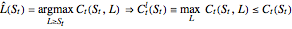 .
.
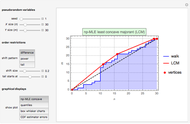
The determination of 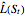 is a simple univariate differentiable optimization problem for any given
is a simple univariate differentiable optimization problem for any given 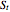 . In this Demonstration, Mathematica's built-in function NMaximize is applied.
. In this Demonstration, Mathematica's built-in function NMaximize is applied.
The evaluation of the capped call payoff function derivative with respect to the cap, while the underlying asset price approaches the cap from below, leads to an exercise boundary 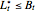 , where
, where 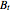 is the American call optimal early exercise boundary at time
is the American call optimal early exercise boundary at time  . The boundary
. The boundary 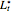 is the solution to the equation
is the solution to the equation 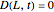 , where
, where 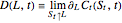 .
.
In this Demonstration, the Newton–Raphson technique is applied to solve 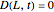 . Moreover, M. Broadie and J. Detemple [1] prove that an upper bound
. Moreover, M. Broadie and J. Detemple [1] prove that an upper bound 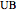 for the American call price is obtained, after replacing the optimal early exercise boundary function
for the American call price is obtained, after replacing the optimal early exercise boundary function 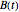 with
with 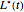 in Kim's integral equation [2]. The integral in Kim's equation represents the early exercise premium and is approximated by Simpson's rule.
in Kim's integral equation [2]. The integral in Kim's equation represents the early exercise premium and is approximated by Simpson's rule.
References
[1] M. Broadie and J. Detemple, "American Option Valuation: New Bounds, Approximations, and a Comparison of Existing Methods," The Review of Financial Studies, 9(4), 1996 pp. 1211–1250.
[2] I. J. Kim, “The Analytic Valuation of American Options,” The Review of Financial Studies, 3(4), 1990 pp. 547–572.
[3] M. Broadie and J. Detemple, "American Capped Call Options on Dividend Paying Assets," The Review of Financial Studies, 8(1), 1995 pp. 161–191.
Permanent Citation