Pricing American Options with the Lower-Upper Bound Approximation (LUBA) Method

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
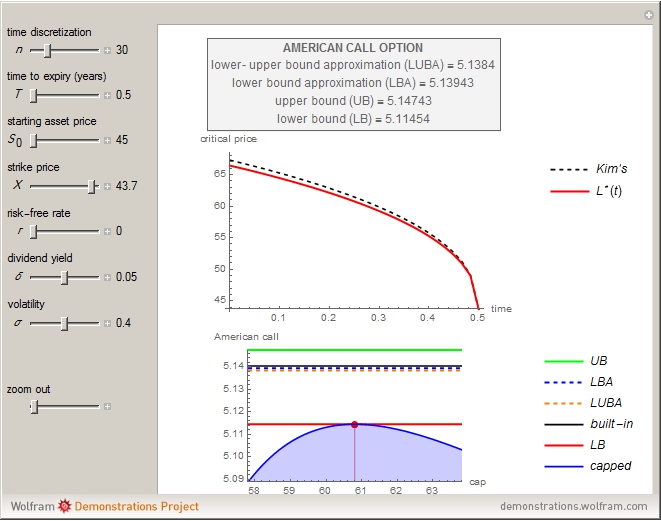
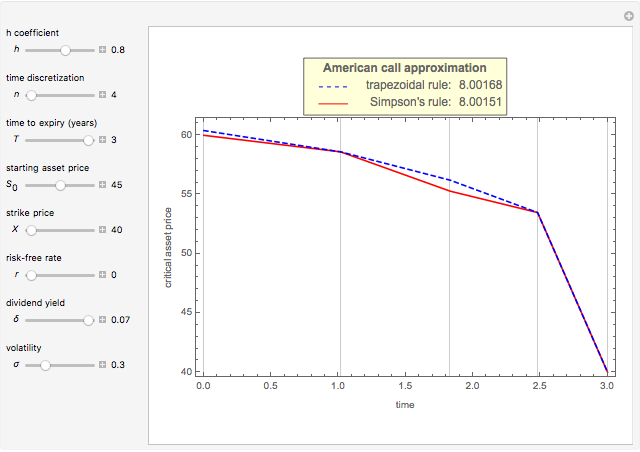
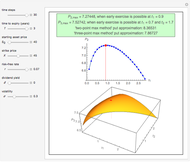
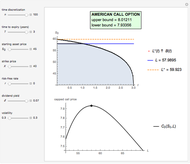
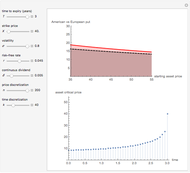
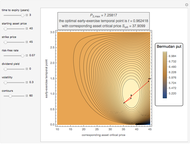
This Demonstration shows the lower and upper bound approximation methods [3] for an American call option.
[more]
Contributed by: Michail Bozoudis (October 2014)
Suggested by: Michail Boutsikas
Open content licensed under CC BY-NC-SA
Snapshots
Details
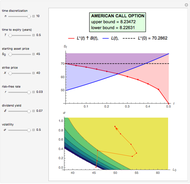
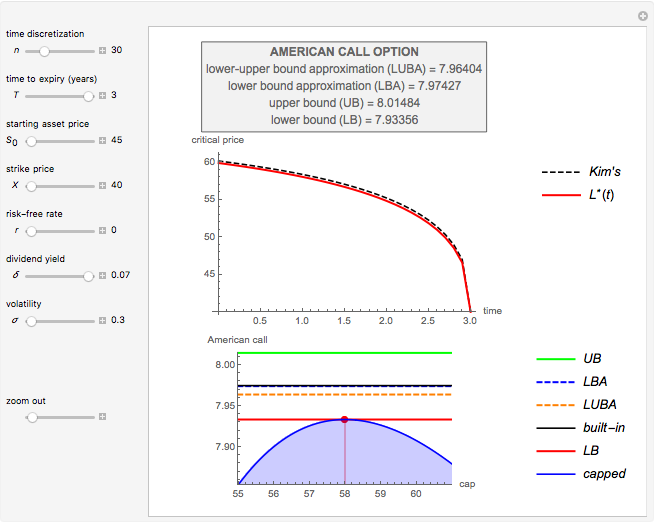
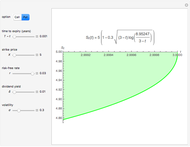
The boundary 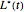 derives from the maximized payoff function [2] for an American capped call.
derives from the maximized payoff function [2] for an American capped call.
The table shows, at  :
:
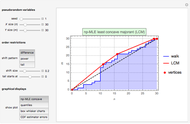
• The American call according to the "lower-upper bound approximation (LUBA)" [3], an empirical approximation method deriving from a weighted average of the option's upper (UB) and lower (LB) bounds,
• The American call according to the "lower bound approximation (LBA)" [3], an empirical approximation method deriving from the option's lower bound (LB),
• The American call upper bound (UB) [3], deriving from Kim's integral equation [1] where 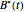 is replaced by
is replaced by 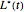 ,
,
• The American call lower bound (LB) [3], deriving from the maximized payoff function of an American capped call.
M. Broadie and J. Detemple [2] developed an analytical formula to estimate American capped call options and they proved that their value could never exceed the value of American call options [3]. Conclusively, the maximized value of an American capped call option is a lower bound (LB) approach for an American call option. The LB approach leads to a boundary 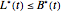 , where
, where 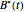 is the American call optimal early exercise boundary function over time. Moreover, M. Broadie and J. Detemple use Kim's integral equation [1] for the early exercise premium; after replacing the optimal early exercise boundary function
is the American call optimal early exercise boundary function over time. Moreover, M. Broadie and J. Detemple use Kim's integral equation [1] for the early exercise premium; after replacing the optimal early exercise boundary function 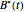 with
with 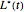 in the integral equation, the result is an upper bound (UB) for the American call. Finally, after examining a large number of options and using regression analysis, they developed two empirical methods (LBA and LUBA) to get more accurate approximations for the American call option.
in the integral equation, the result is an upper bound (UB) for the American call. Finally, after examining a large number of options and using regression analysis, they developed two empirical methods (LBA and LUBA) to get more accurate approximations for the American call option.
References
[1] I. Kim, “The Analytic Valuation of American Options,” Review of Financial Studies, 3(3), 1990 pp. 547–572.
[2] M. Broadie and J. Detemple, "American Capped Call Options on Dividend Paying Assets," Review of Financial Studies, 8(1), 1995 pp. 161–191.
[3] M. Broadie and J. Detemple, "American Option Valuation: New Bounds, Approximations, and a Comparison of Existing Methods," Review of Financial Studies, 9(4), 1996 pp. 1211–1250.
Permanent Citation