Lewis Carroll's Bilateral Diagram

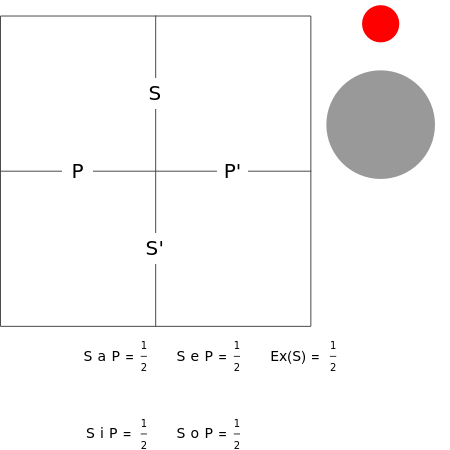
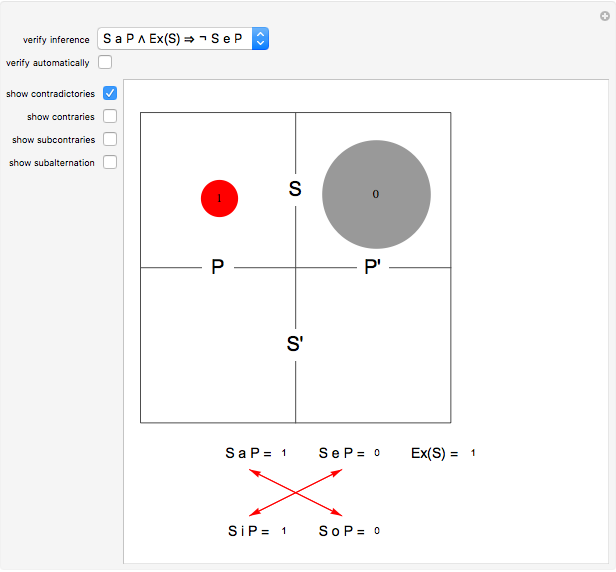
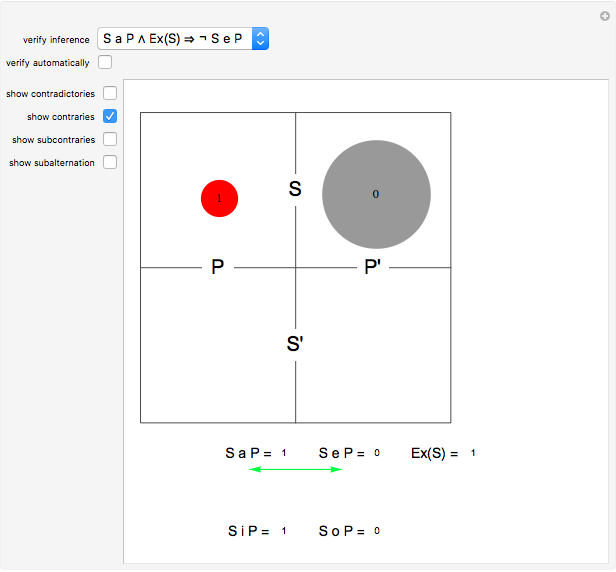
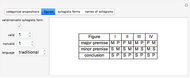
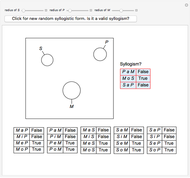
Aristotelian logic, or the traditional study of deduction, deals with four so-called categorical or subject-predicate propositions, which can be defined by:
S a P ⇔ All S is P (universal affirmative or A proposition),
S i P ⇔ Some S is P (particular affirmative or I proposition),
S e P ⇔ No S is P (universal negative or E proposition),
S o P ⇔ Some S is not P (particular negative or O proposition).

S is called a subject (or minor) term and P is called a predicate (or major) term of a proposition. We could think of S and P as one-place predicates or sets.

The bilateral diagram is a way to understand relations among categorical propositions. It
is a square divided into four smaller square cells: SP, SP', S'P, S'P'. A red counter (or 1) within a cell means that there is at least one thing in it. A gray counter (or 0) within a cell means there is nothing in it. So we may not put both counters in the same cell. A red counter in the cell SP means "Some S is P"; a gray counter in the cell SP means "No S is P". The red counter in the upper rectangle means that there is at least one S, symbolically Ex(S) ⇔ S i S. But if we put the counter on the common line of squares SP and SP', we don't know whether the proposition S i P is true (1) or false (0), so it has value unknown or undetermined (½). The same holds for S o P. Analogously, the value of the proposition S a P is ½ , unless we put the gray counter in the square SP' (S a P = 1) or in SP (S a P = 0).