Venn Diagrams and Syllogisms

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
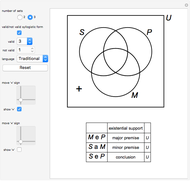
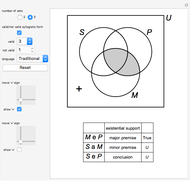
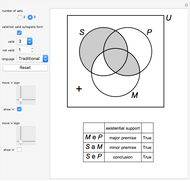
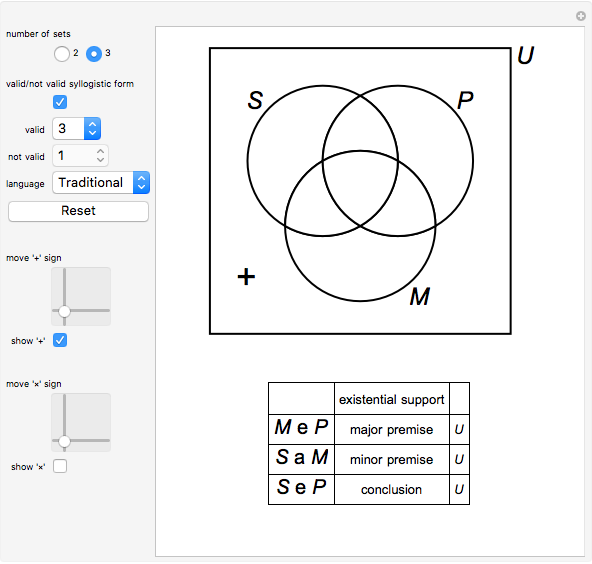
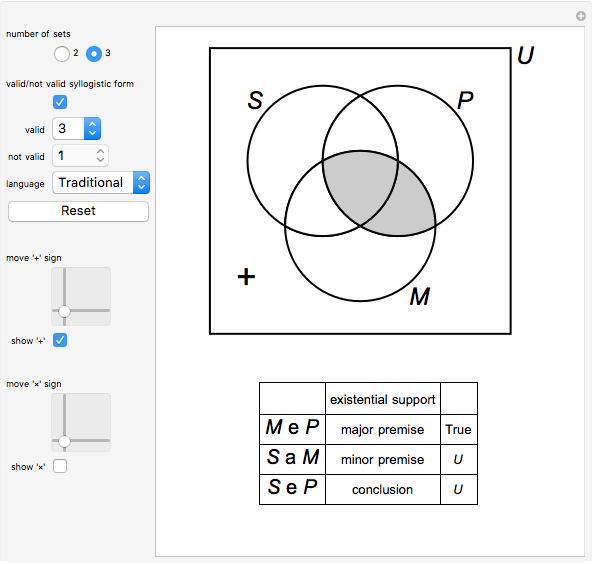
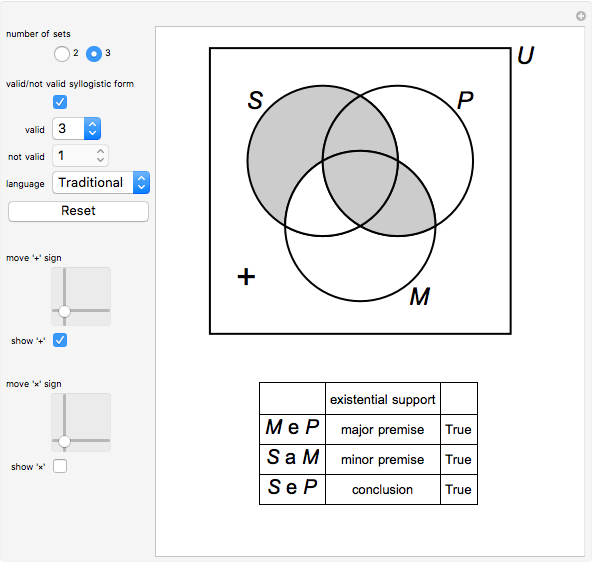
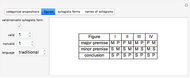
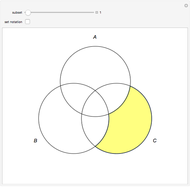
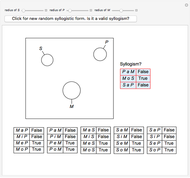
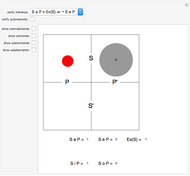
This Demonstration lets you verify 24 valid syllogisms using Venn diagrams with only one element in the domain. The domain only needs two elements, denoted by "+" and "×", to show that a syllogistic form is not valid.
[more]
Contributed by: Izidor Hafner (August 2016)
using code written by Marc Brodie
Open content licensed under CC BY-NC-SA
Snapshots
Details
A monadic formula of first-order logic is one for which all nonlogical symbols are one-place predicates.
Theorem. If  is a monadic sentence that is satisfiable, then
is a monadic sentence that is satisfiable, then  is true in some interpretation whose domain contains at most
is true in some interpretation whose domain contains at most  members, where
members, where  is the number of one-place predicate letters and
is the number of one-place predicate letters and  is the number of variables in
is the number of variables in  .
.
Therefore there is an effective procedure for deciding whether or not a monadic sentence is valid [1, p. 250].
Syllogistic forms are monadic sentences if considered as sentences of the form  with predicate letters
with predicate letters  ,
,  , and
, and  .
.
References
[1] G. S. Boolos and R. C. Jeffrey, Computability and Logic, Cambridge, UK: Cambridge University Press, 1974.
[2] L. Carroll, Symbolic Logic and The Game of Logic, New York: Dover Publications, 1958.
[3] I. M. Copi and C. Cohen, Introduction to Logic, 9th ed., New York: Macmillan Publishers, 1994 pp. 214–218.
[4] J. M. Boche\:0144ski, A History of Formal Logic, 2nd ed. (I. Thomas, trans. and ed.), New York: Chelsea Publishing Company, 1970 p. 235.
[5] Wikipedia. "Syllogism." (Aug 3, 2016) en.wikipedia.org/wiki/Syllogism.
[6] Wikipedia. "Venn Diagram." (Aug 3, 2016) en.wikipedia.org/wiki/Venn_diagram.
[7] J. Venn, "On the Diagrammatic and Mechanical Representation of Propositions and Reasonings," Philosophical Magazine Series 5, 10(59), 1880 pp. 1–18. doi:10.1080/14786448008626877.
Permanent Citation