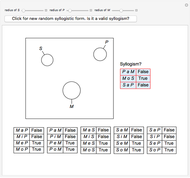
Lewis Carroll's Diagram and Categorical Syllogisms

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
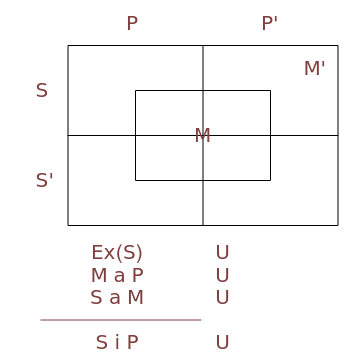
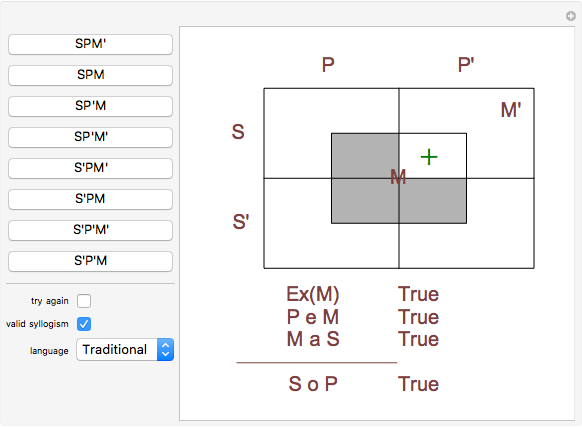
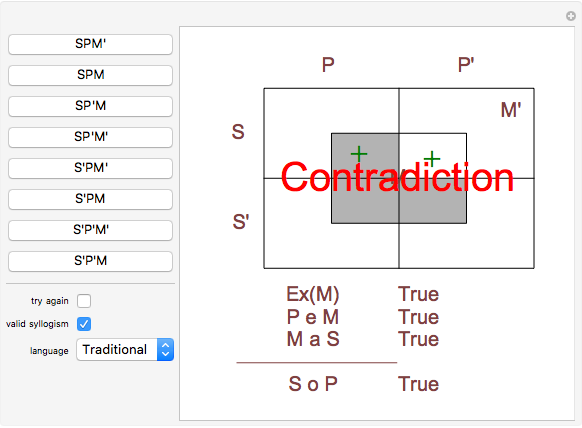
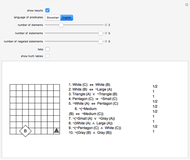
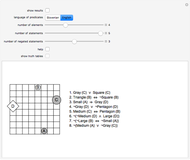
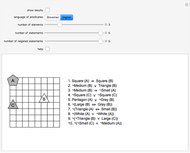
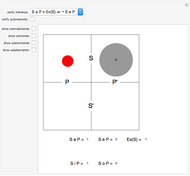
Aristotelian logic, or the traditional study of deduction, deals with four so-called categorical or subject-predicate propositions, which can be defined by S a P ⇔ All S is P (universal affirmative or A proposition), S i P ⇔ Some S is P (particular affirmative or I proposition), S e P ⇔ No S is P (universal negative or E proposition), S o P ⇔ Some S is not P (particular negative or O proposition).
[more]
Contributed by: Izidor Hafner (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The so-called figure of a categorical syllogism is determined by the possible position of middle term. There are four figures:
M x P, S x M ⊨ S x P, P x M, S x M ⊨ S x P, M x P, M x S ⊨ S x P, P x M, M x S ⊨ S x P, where x is a, i, e, or o.
This version of Carroll's diagrams was found in [2], p. 112. See also the Wikipedia entry for Categorical proposition.
[1] R. Audi, ed., The Cambridge Dictionary of Philosophy, Cambridge: Cambridge University Press, 1995 pp. 780–782. [2] L. Borkowski, Elementy logiki formalnej (Elements of Formal Logic, in Polish), 3rd ed., Warsaw: Wyd, 1976. [3] L. Carroll, Symbolic Logic and the Game of Logic, New York: Dover, 1958. [4] I. M. Copi and C. Cohen, Introduction to Logic, 9th ed., New York: Macmillan, 1994 pp. 214–218.
Permanent Citation
"Lewis Carroll's Diagram and Categorical Syllogisms"
http://demonstrations.wolfram.com/LewisCarrollsDiagramAndCategoricalSyllogisms/
Wolfram Demonstrations Project
Published: March 7 2011