Mamikon's Method for the Area of the Cycloid
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
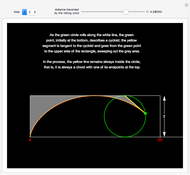
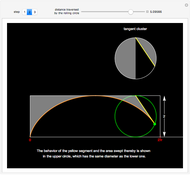
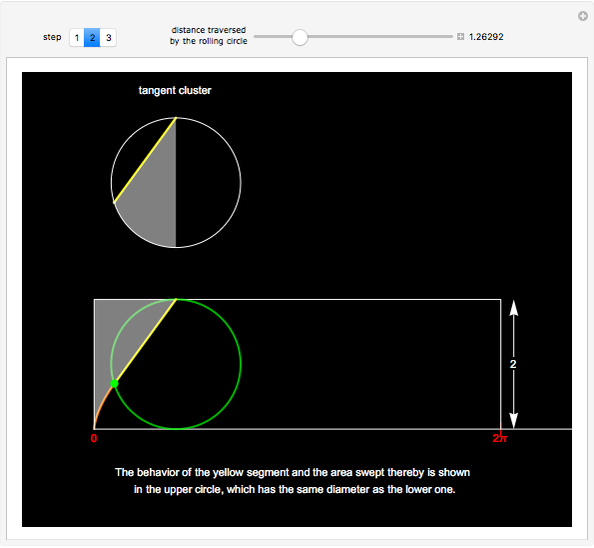
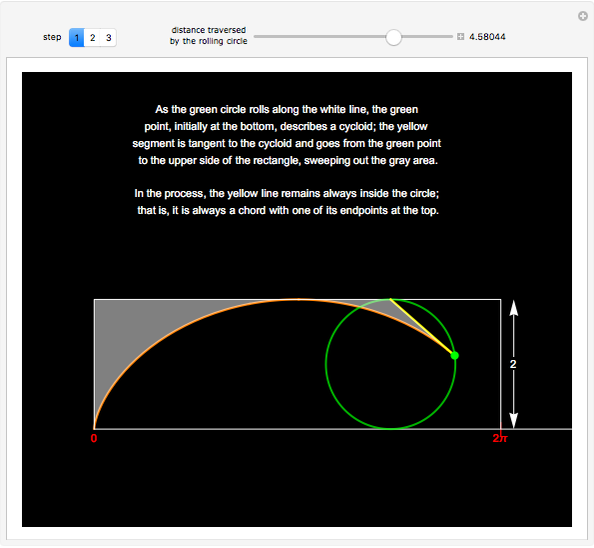
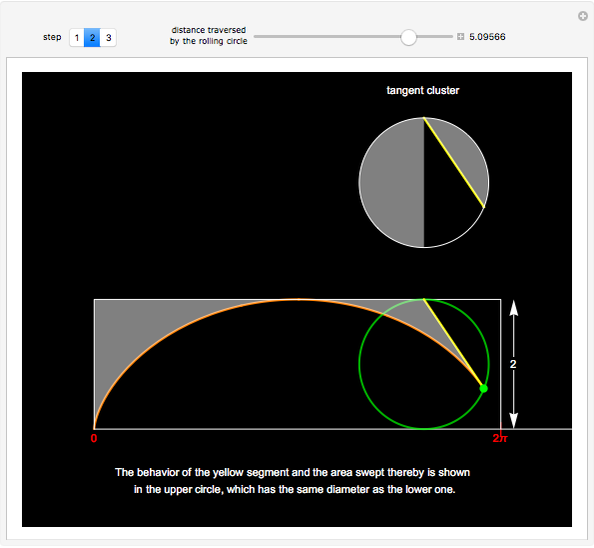
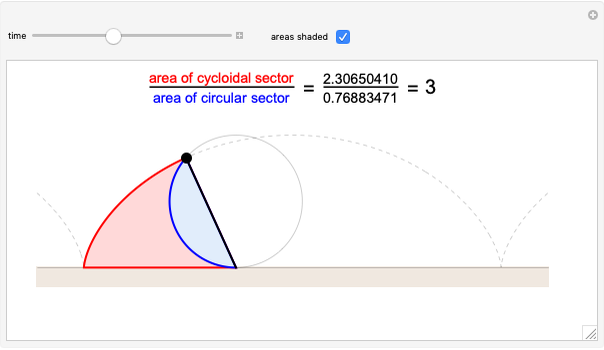
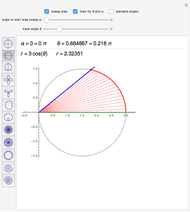
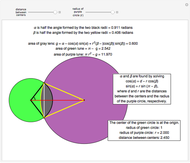
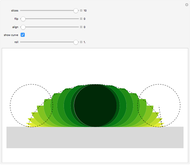
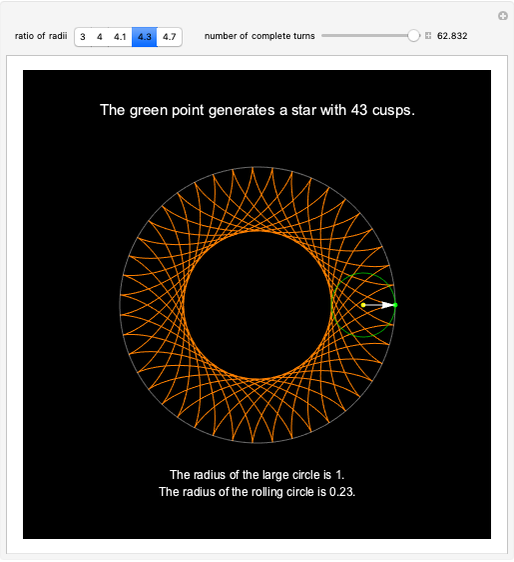
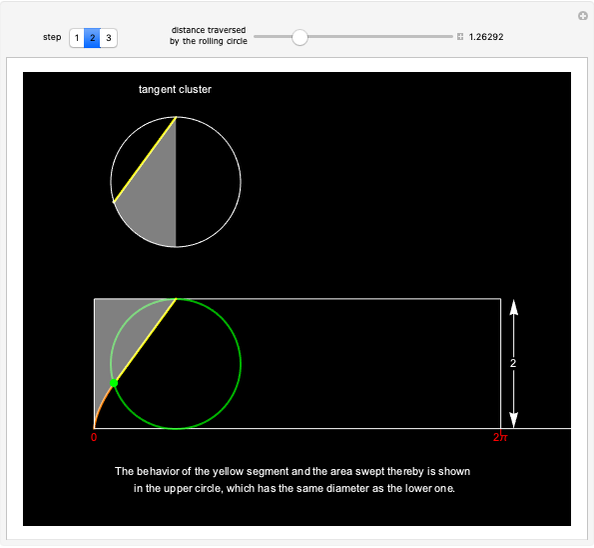
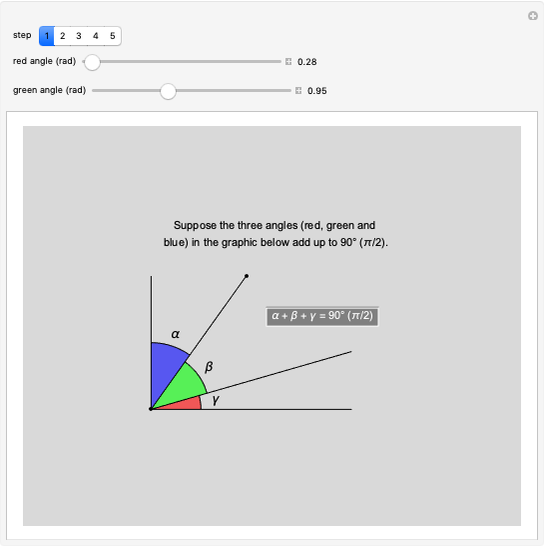
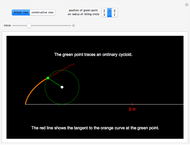
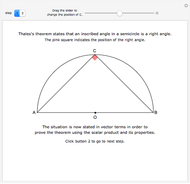
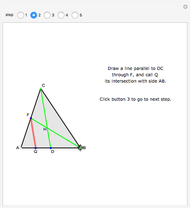
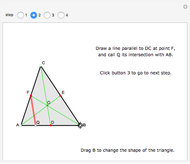
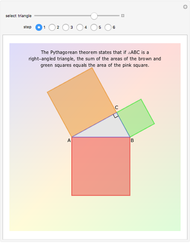
The area under the curve traced by a point at the end of the diameter of a circle with radius 1—a cycloid—is determined using only geometric concepts.
Contributed by: Tomas Garza (November 2019)
Open content licensed under CC BY-NC-SA
Details
In 1959, Mamikon Mnatsakanian, usually known as Mamikon, devised an original method for solving problems in geometry. His method is described in [1].
In this Demonstration, an example is presented based on work by Ujjwal Rane [2], where the area of the cycloid is obtained without recourse to the methods of calculus.
References
[1] Wikipedia. "Visual Calculus." (Nov 4, 2019) en.wikipedia.org/wiki/Visual_calculus.
[2] U. Rane. Geometry with MicroStation Mamikon's Theorem [Video]. (Nov 4, 2019) www.youtube.com/watch?v=sjqKfuuDZqA.
Snapshots
Permanent Citation
Area under a Cycloid
Okay Arik
Cumulative Area under a Cycloid versus the Area of Its Rolling Circle
Ken Caviness
Triangle Area Bisectors
Ismail Hammoudeh
Polar Area Sweep
Abby Brown
Area Under the Tractrix
Okay Arik
The Medians of a Triangle Divide It into Three Smaller Triangles of Equal Area
Tomas Garza
Areas of the Lens and Two Lunes of Two Intersecting Circles
Tomas Garza
Area under a Cycloid (II)
Okay Arik
Area under the Exponential Curve
Okay Arik
Area under a Parabola by Symmetries
Gerry Harnett
-
Hypocycloids
Tomas Garza -
Generating a Hyperbola Using Steiner's Method
Tomas Garza -
Simple Nomogram for 95% Confidence Intervals in Small-Sample Binomial Statistics
Tomas Garza -
Mamikon's Method for the Area of the Cycloid
Tomas Garza -
Area of an Inscribed Triangle in Terms of the Product of Its Sides
Tomas Garza -
Visual Derivation of a Trigonometric Identity
Tomas Garza -
Observed Distribution of Random Chord Lengths in a Circle
Tomas Garza -
Constructing an Ellipse with a Tusi Couple
Tomas Garza -
Cycloids and Their Tangents
Tomas Garza -
Stratification as a Device for Variance Reduction
Tomas Garza -
Intersection of Two Lines Using Vectors
Tomas Garza -
Areas of the Lens and Two Lunes of Two Intersecting Circles
Tomas Garza -
Cosine and Sine of the Sum of Two Angles
Tomas Garza -
Thales's Theorem: A Vector-Based Proof
Tomas Garza -
The Medians of a Triangle Divide It into Three Smaller Triangles of Equal Area
Tomas Garza -
The Medians of a Triangle Are Concurrent: A Visual Proof
Tomas Garza -
The Centroid of a Triangle Divides Each Median in the Ratio 1:2
Tomas Garza -
Da Vinci's Proof of the Pythagorean Theorem
Tomas Garza -
Confidence Intervals, Confidence Levels, and Average Interval Length
Tomas Garza -
Confidence Intervals for the Binomial Distribution
Tomas Garza