Simple Nomogram for 95% Confidence Intervals in Small-Sample Binomial Statistics

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
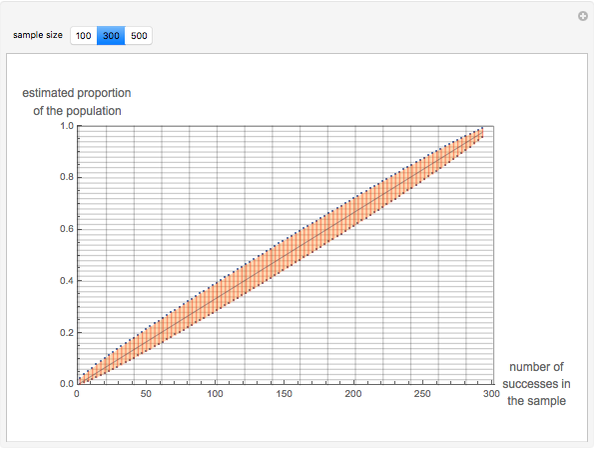
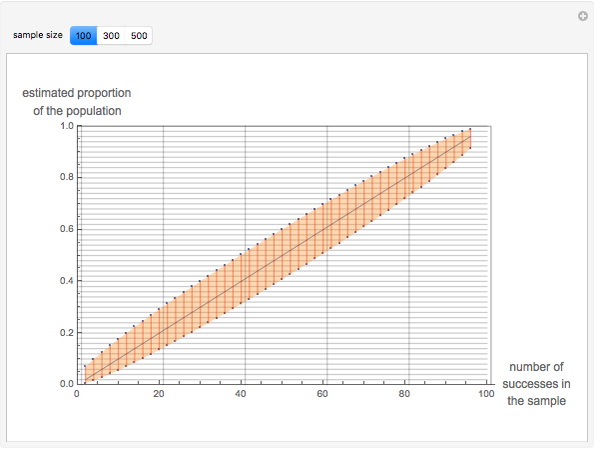
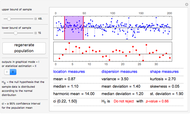
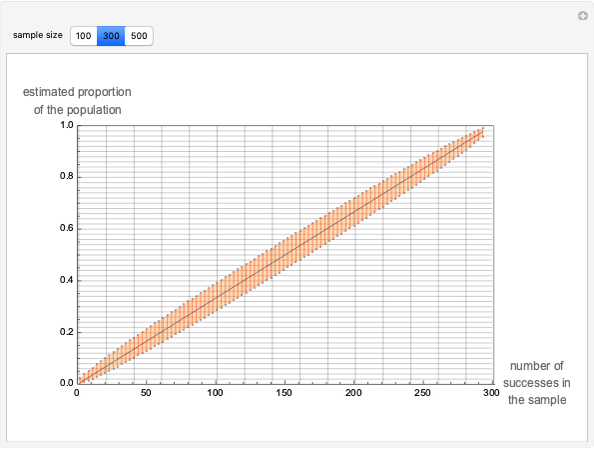
Exact confidence intervals for the proportion parameter in a binomial setup are presented graphically, for a confidence level of 95%. Three examples are shown, corresponding to sample sizes of 100, 300 and 500. Hover the cursor over the points in the graph to see the point estimate, as well as the upper and lower values of the intervals for the possible outcomes of the sampling process.
Contributed by: Tomas Garza (November 2019)
Open content licensed under CC BY-NC-SA
Details
Nomograms are graphical representations of mathematical relationships or laws. A detailed review of this topic appears in [1].
In this Demonstration, a graphical representation is given to provide interval estimates for a small-sample binomial scheme, based on the Clopper–Pearson method [2, 3]. A fixed 95% confidence level is used for the three sample sizes. The performance of the method has been studied in [4].
References
[1] R. Doerfler. "The Art of Nomography I: Geometric Design," Dead Reckonings: Lost Art in the Mathematical Sciences (blog). (Nov 18, 2019) myreckonings.com/wordpress/2008/01/09/the-art-of-nomography-i-geometric-design.
[2] Wikipedia. "Binomial Proportion Confidence Interval." (Nov 18, 2019) en.wikipedia.org/wiki/Binomial_proportion_confidence_interval.
[3] M. Thulin, "The Cost of Using Exact Confidence Intervals for a Binomial Proportion," Electronic Journal of Statistics, 8(1), 2014 pp. 817–840. doi:10.1214/14-EJS909.
[4] T. Garza. "Confidence Intervals, Confidence Levels and Average Interval Length" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/ConfidenceIntervalsConfidenceLevelsAndAverageIntervalLength.
Snapshots
Permanent Citation