Maximizing a Bermudan Put with Two Early-Exercise Temporal Points

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
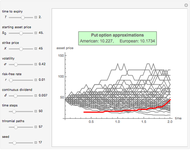
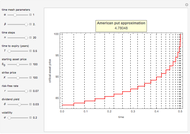
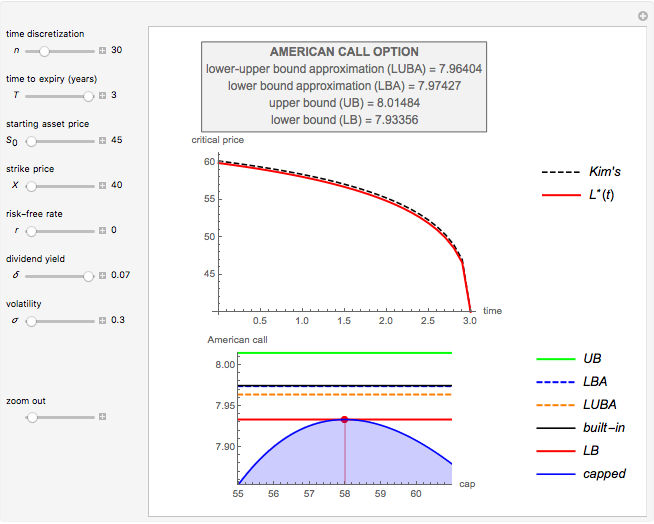
This Demonstration locates the optimal early-exercise temporal points and the corresponding asset critical prices that maximize the value of a Bermudan put with two possible early-exercise temporal points. While European options can be exercised only at the date of expiration, Bermudan options extend the notion of exercise to a finite number of time points during their life. American options, which can be exercised at any time up to maturity, can be approximated (bounded from below) by considering Bermudan options, where the number of early-exercise points becomes considerably dense.
Contributed by: Michail Bozoudis (October 2014)
Suggested by: Michail Boutsikas
Open content licensed under CC BY-NC-SA
Snapshots
Details
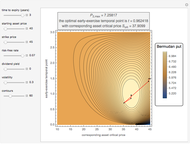
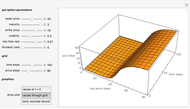
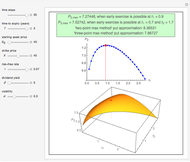
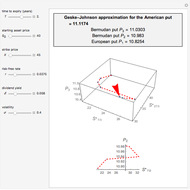
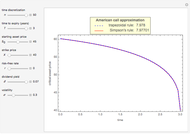
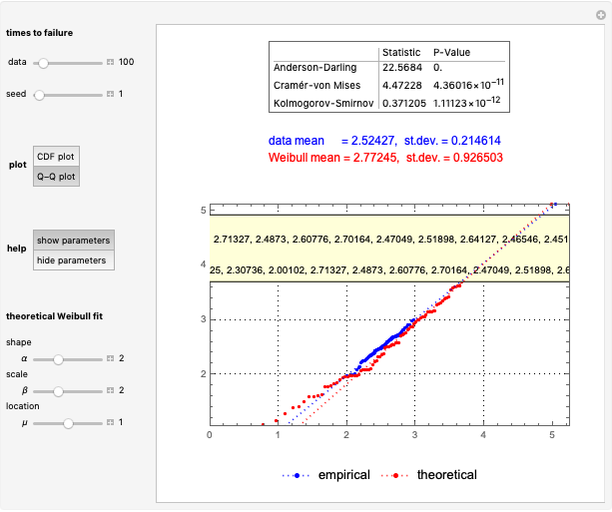
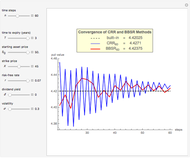
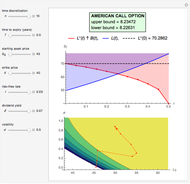
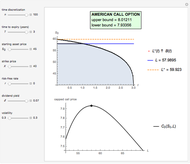
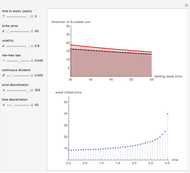
Use the controls to select the Bermudan put parameters, and then monitor how the optimal temporal points are reached step by step, with Mathematica's built-in function FindMaximum (upper graph); you can use the last control to reset the starting time points. The lower graph shows the Bermudan optimal early-exercise temporal points and their corresponding critical prices (red dots), compared to the early-exercise boundary of the American put (blue line), according to Mathematica's built-in function FinancialDerivative.
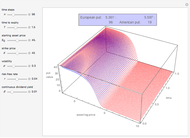
The Geske–Johnson analytical formula [1] is applied to estimate the payoff function of the Bermudan put. The goal of the optimization process is to find the two early-exercise time points at which the payoff function of the option is maximized; these times are related to corresponding asset critical prices, as in the case of American options.
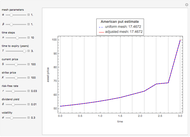
Geske and Johnson, in the "G–J" method [1], apply Richardson extrapolation on uniformly time-discretized Bermudan options to approximate the value of an American option. Bunch and Johnson, in the "two-point maximum" and "three-point maximum" approximation methods [2], suggest using optimally time-discretized Bermudan options instead, in order to get a better approximation for the American option.
References
[1] R. Geske and H. Johnson, "The American Put Option Valued Analytically," The Journal of Finance, 39(5), 1984 pp. 1511–1524. doi:10.1111/j.1540-6261.1984.tb04921.x.
[2] D. Bunch and H. Johnson, "A Simple and Numerically Efficient Valuation Method for American Puts Using a Modified Geske–Johnson Approach," The Journal of Finance, 47(2), 1992 pp. 809–816. doi:10.1111/j.1540-6261.1992.tb04412.x.
Permanent Citation
"Maximizing a Bermudan Put with Two Early-Exercise Temporal Points"
http://demonstrations.wolfram.com/MaximizingABermudanPutWithTwoEarlyExerciseTemporalPoints/
Wolfram Demonstrations Project
Published: October 3 2014