12,000+ Interactive Demonstrations Powered by Notebook Technology »

Melvyn Knight's Problem

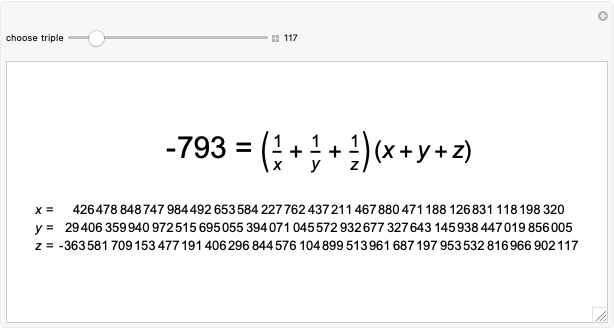
Melvyn Knight once asked [1] for which integers is there an integer triple so that .
For example, 11 has two such representations: and .
Solutions for this problem can be found using elliptic curves [1]. This Demonstration shows a sample solution for all solvable values from to . When one solution exists, there are an infinite number of solutions.

SNAPSHOTS

  • [Snapshot]
  • [Snapshot]
  • [Snapshot]

DETAILS

The original problem [1]
may be rewritten as
,
and further rewritten as
.
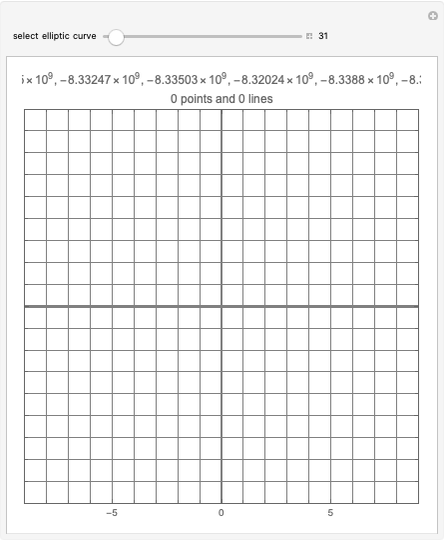
Solving for leads to a complicated expression equivalent to the elliptic curve:
.
A tabulation of the integers that can be represented is given in [2].
References
[1] A. Bremner, R. K. Guy and R. J. Nowakowski, "Which Integers Are Representable as the Product of the Sum of Three Integers with the Sum of Their Reciprocals?," Mathematics of Computation, 61(203), 1993 pp. 117–130. www.ams.org/journals/mcom/1993-61-203/S0025-5718-1993-1189516-5/S0025-5718-1993-1189516-5.pdf.
[2] H. Pfoertner. "Integers n representable as the product of the sum of three nonzero integers with the sum of their reciprocals." The On-Line Encyclopedia of Integer Sequences. (Jan 24, 2023) oeis.org/A085514.

PERMANENT CITATION

 Ed Pegg Jr
"Melvyn Knight's Problem"
 http://demonstrations.wolfram.com/MelvynKnightsProblem/
 Wolfram Demonstrations Project
 Published: January 26, 2023
    • Share:

Embed Interactive Demonstration New!

Just copy and paste this snippet of JavaScript code into your website or blog to put the live Demonstration on your site. More details »

Files require Wolfram CDF Player or Mathematica.





Related Topics