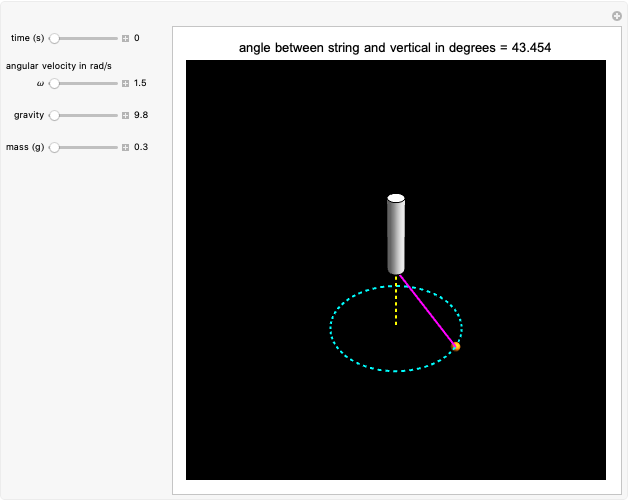
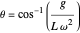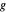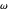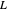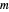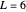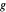Motion of a Conical Pendulum

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
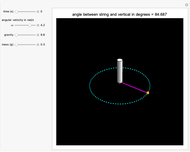
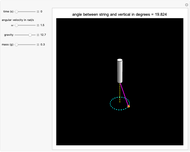
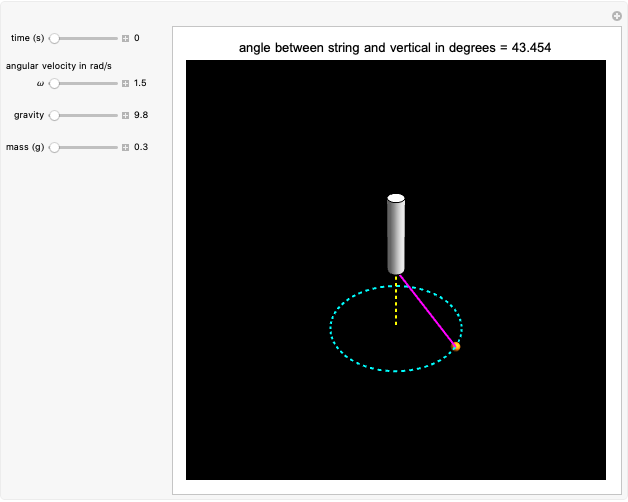
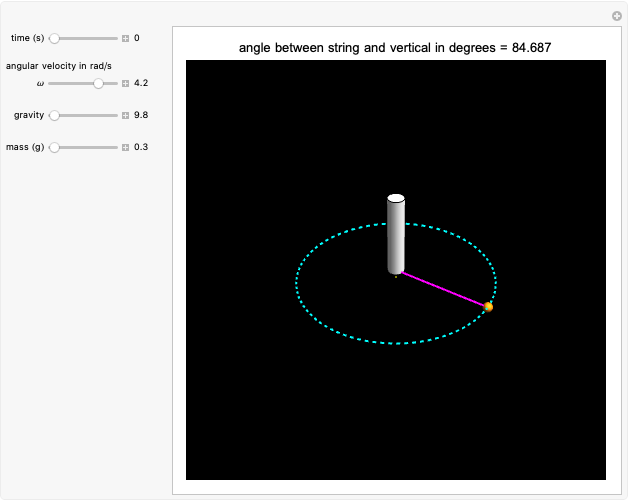
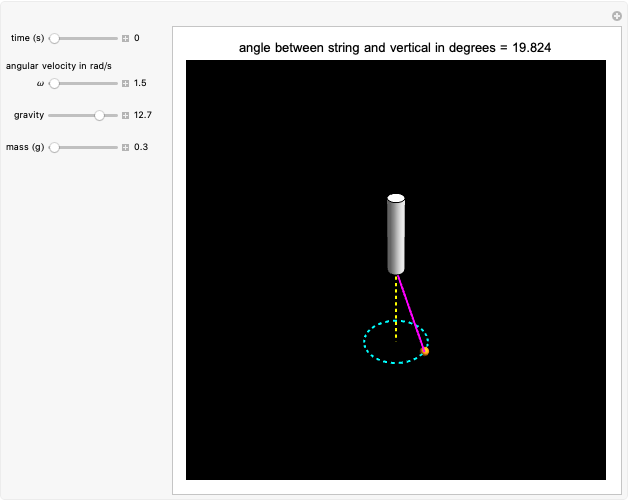
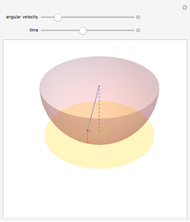
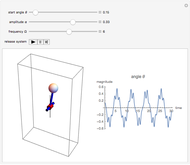
For the conical pendulum, gravity, mass, and the angular velocity determine the angle between the string and the vertical axis of the pendulum.
[more]
Contributed by: Hiroki Nakayama and David Oh. (June 2014)
Open content licensed under CC BY-NC-SA
Details
The upward force produced by the tension 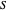 balances the downward force from the weight of the pendulum:
balances the downward force from the weight of the pendulum:
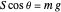 . (1)
. (1)
Also, because the pendulum system is conical, the mass moves in a circular orbit.
In a circular orbit, the pendulum experiences an inward centripetal force given 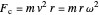 . The horizontal component of tension
. The horizontal component of tension 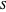 balances this centripetal force:
balances this centripetal force:
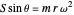 . (2)
. (2)
Dividing (2) by (1):
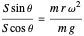 ,
,
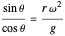 ,
,
 ,
,
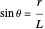 ,
,
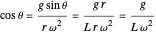 .
.
This means that the angle that the string makes with the vertical depends on the gravity 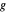 , the length of the string
, the length of the string 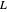 , and the angular velocity,
, and the angular velocity,  .
.
Snapshot 1: as the angular velocity increases, the angle between the string and the vertical increases
Snapshot 2: as gravity increases, the angle between the string and the vertical decreases
Snapshot 3: increasing the mass does not have any effect on the angle
Special thanks to the University of Illinois NetMath Program and the mathematics department at William Fremd High School.
This Demonstration was written with materials from Making Math [1].
References
[1] O'Reilly Media. "Making Math." (Jun 2, 2014) www.makingmath.com.
[2] R. Fitzpatrick. "The Conical Pendulum" in Classical Mechanics: An Introductory Course. (Jun 12, 2014) farside.ph.utexas.edu/teaching/301/lectures/node88.html.
Snapshots
Permanent Citation