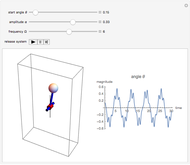
Vibrating Inverted Pendulum
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
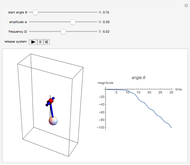
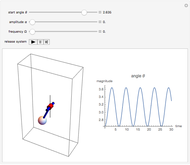
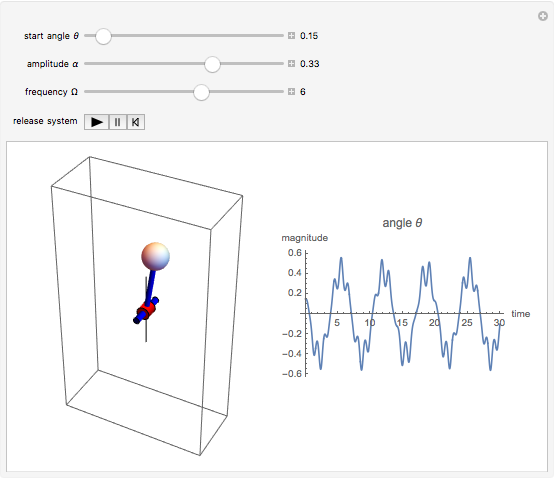
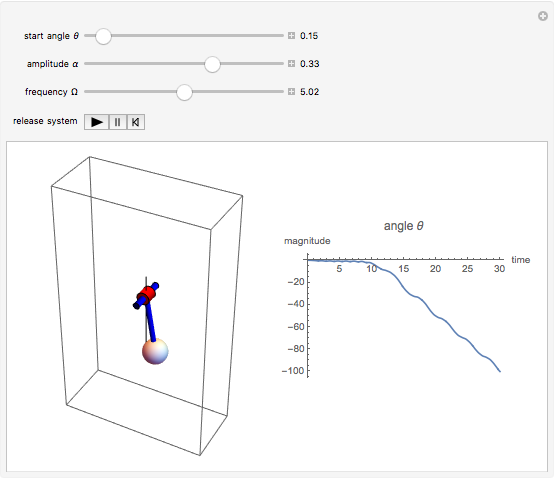
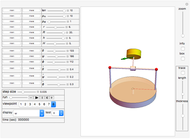
This Demonstration shows an inverted pendulum that vibrates sinusoidally at its base in the vertical direction at some frequency. The normalized vibration frequency is denoted by 
and the normalized vibration amplitude by 
. For some configurations of amplitude and frequency, the pendulum is relatively stable and stays inverted, while at others it starts to tumble. If 
or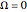 
, you have a simple pendulum. The initial angle 
is measured from the vertical at time 0.
Contributed by: Kay Herbert (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
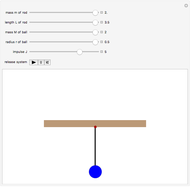
The inverted pendulum is modeled as a point mass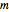 
on a rod of length 
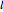with a vertical sinusoidal excitation of amplitude 
and frequency 
at the origin.
The position of the mass 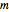is then given by
, 
.
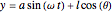The forces in the 
and 
direction are then
, 
,
where 
is the acceleration of gravity.
With the force acting only in the direction of the rod,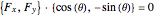 
.
The equation for becomes
,
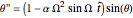where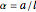 
, 
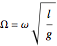, and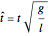 
.
Reference
[1] J. P. Den Hartog, Mechanical Vibrations, New York: McGraw–Hill, 1956.
Permanent Citation
Torsion Pendulum
Enrique Zeleny
Pendulum Waves
Stan Wagon (Macalester College) and S. M. Blinder
Conic Pendulum
Enrique Zeleny
Impulse Acting on a Pendulum
Sarah Lichtblau
Rigid Body Pendulum on a Flywheel
Nasser M. Abbasi
Normal Modes of a Double Pendulum
David L. Pincus
Conservation of Energy with a Simple Pendulum
S. E. McCaslin
Spinning Disk Pendulum Swinging on Top of a Rotating Table
Nasser M. Abbasi
Torsional Pendulums
Ernest Lee
Spherical Pendulum
Franz Krafft
