Normalized B-Bases for Trigonometric Polynomial Curves

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
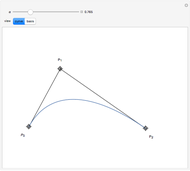
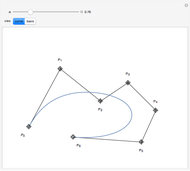
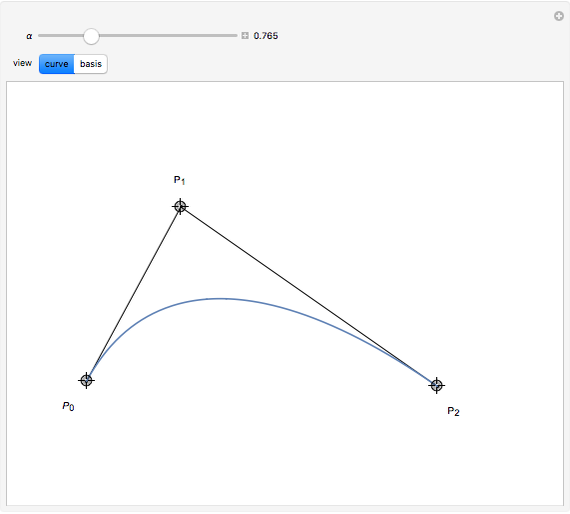
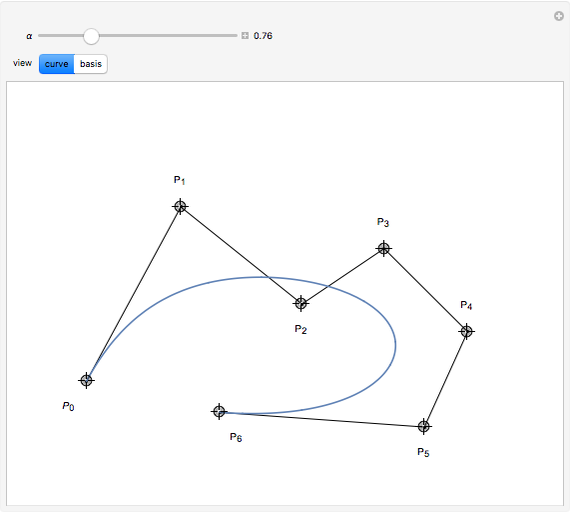
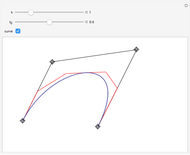
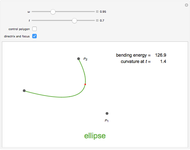
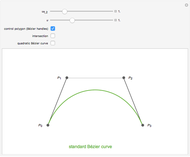
B-curves are trigonometric polynomial curves; they are plots of linear combinations of a B-basis, which generalizes the polynomial Bernstein basis. B-curves can easily be controlled and modified by a control polygon, very much like the more common Bézier curves.
Contributed by: Isabelle Cattiaux-Huillard and Gudrun Albrecht (February 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
A classical function space is the order- trigonometric polynomial space
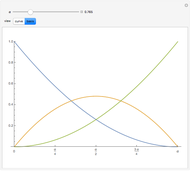
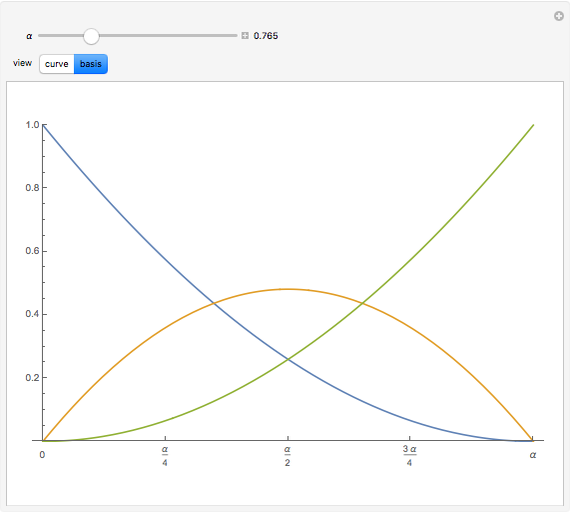
trigonometric polynomial space  . The following is a normalized B-basis for such a space, for
. The following is a normalized B-basis for such a space, for  [1]:
[1]:
 ,
,
with
 .
.
This basis allows the definition of a B-curve by
 ,
,
where  is the control polygon.
is the control polygon.
In this Demonstration, we plot such B-curves, with an adjustable (odd) number of control points. You can also vary the value of  and see the corresponding normalized B-basis as well. The order
and see the corresponding normalized B-basis as well. The order  of this basis corresponds to the number of control points, which has to be odd for the B-curve and its basis to exist.
of this basis corresponds to the number of control points, which has to be odd for the B-curve and its basis to exist.
Reference
[1] J. Sanchez–Reyes, "Harmonic Rational Bézier Curves,  -Bézier Curves and Trigonometric Polynomials," Computer Aided Geometric Design, 15, 1998 pp. 909–923. doi.10.1016/S0167-8396(98)00031-4.
-Bézier Curves and Trigonometric Polynomials," Computer Aided Geometric Design, 15, 1998 pp. 909–923. doi.10.1016/S0167-8396(98)00031-4.
Permanent Citation