Pythagorean-Hodograph (PH) Cubic Curves

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
A polynomial curve  is a Pythagorean-Hodograph (PH) curve if
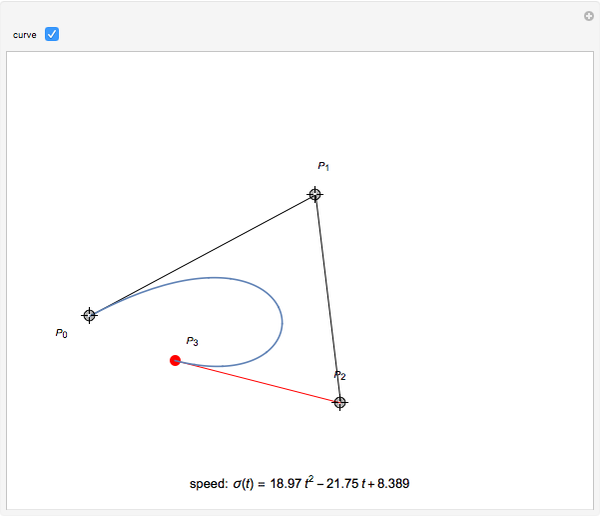
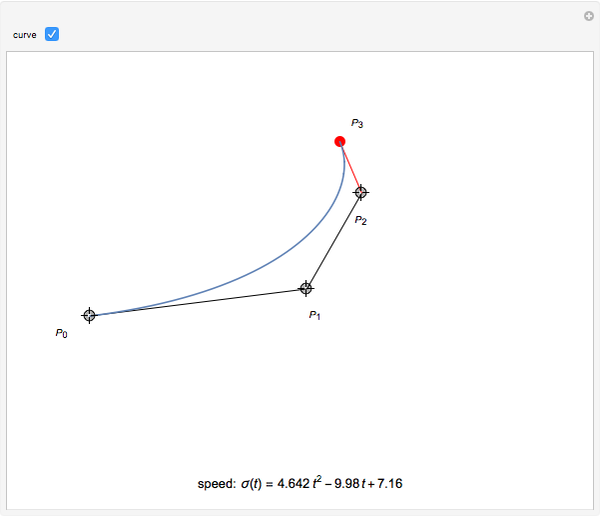
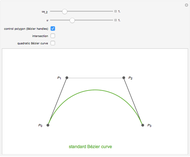
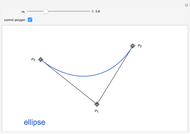
is a Pythagorean-Hodograph (PH) curve if  is the square of another polynomial. The lowest-degree curves satisfying this condition are PH-cubics, here presented in Bézier form. The degrees of freedom of such a curve let you choose three of the four control polygon points. The remaining point is then determined.
is the square of another polynomial. The lowest-degree curves satisfying this condition are PH-cubics, here presented in Bézier form. The degrees of freedom of such a curve let you choose three of the four control polygon points. The remaining point is then determined.
Contributed by: Isabelle Cattiaux-Huillard and Gudrun Albrecht (March 2014)
Open content licensed under CC BY-NC-SA
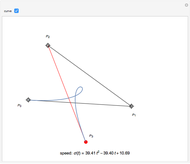
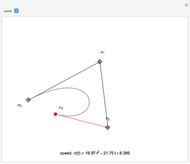
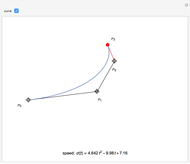
Snapshots
Details
Consider a polynomial parametric curve  . By definition, its hodograph is its derivative
. By definition, its hodograph is its derivative  . It is said to be Pythagorean if there is another polynomial
. It is said to be Pythagorean if there is another polynomial  such that
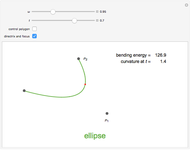
such that  . The curve is then said to have a Pythagorean hodograph, or, for short, to be a PH curve. it has the remarkable properties of having polynomial speed
. The curve is then said to have a Pythagorean hodograph, or, for short, to be a PH curve. it has the remarkable properties of having polynomial speed  and permitting offset curves with rational parametrizations.
and permitting offset curves with rational parametrizations.
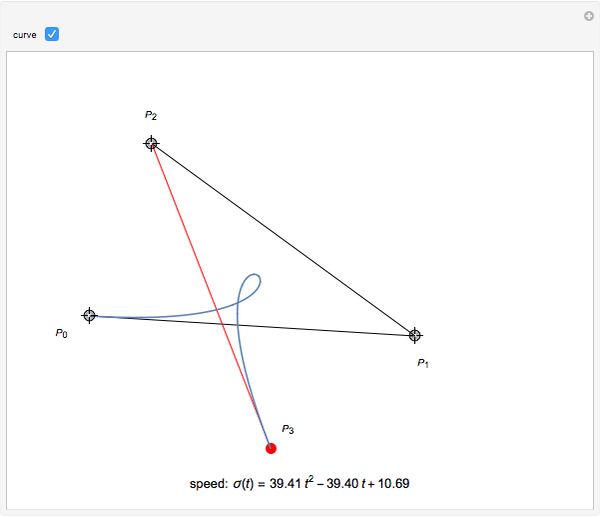
The lowest-degree curve allowing this property is three. Therefore this Demonstration shows cubic curves written in Bézier form, that is, represented by their control polygons  (see [1]).
(see [1]).
Denoting by  the distance between
the distance between  and
and  and by
and by  the angle
the angle 
 , a cubic curve is PH if and only if
, a cubic curve is PH if and only if  and
and  . This result allows the free choice of three of the control points; the fourth one is then determined.
. This result allows the free choice of three of the control points; the fourth one is then determined.
Reference
[1] R. T. Farouki, Pythagorean-Hodograph Curves: Algebra and Geometry inseparable, Berlin: Springer, 2008.
Permanent Citation