Optimal Economic Strategy for the Operation of a Batch Reactor with Dead Time

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
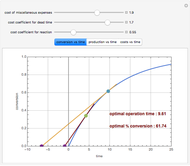
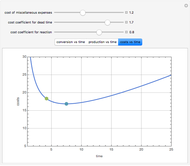
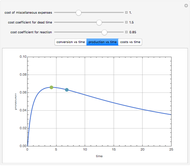
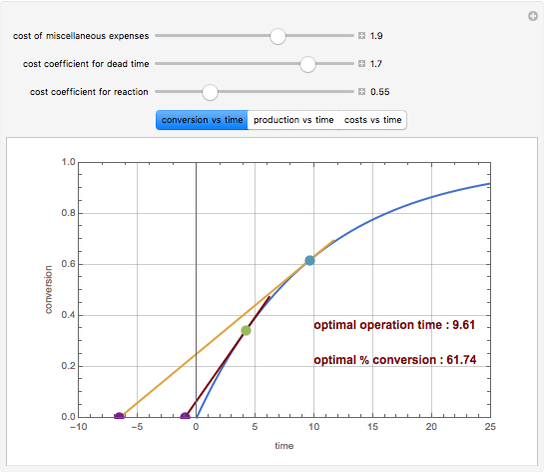
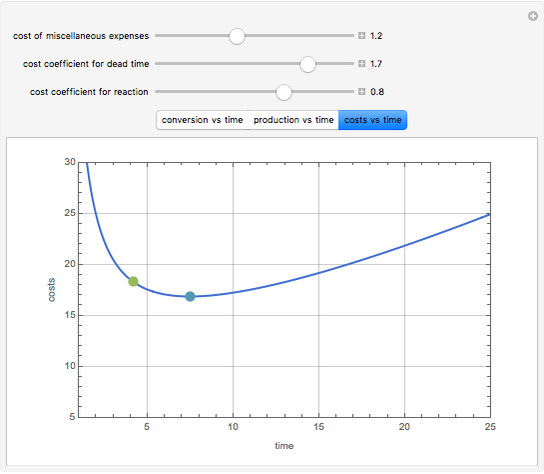
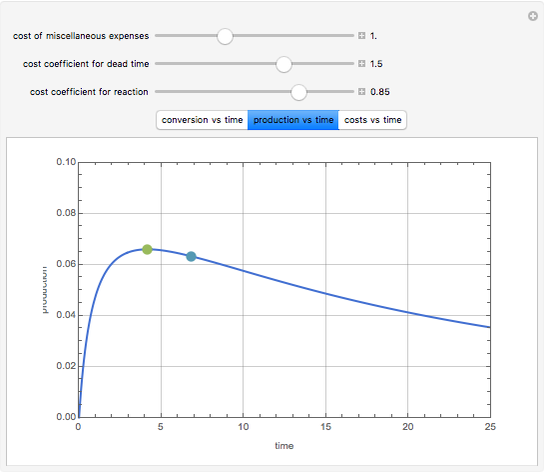
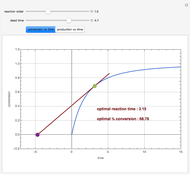
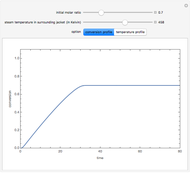
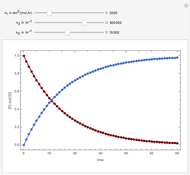
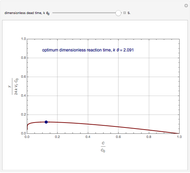
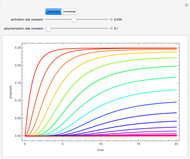
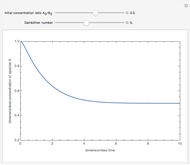
Consider an irreversible first-order reaction  taking place in a batch reactor. The production of
taking place in a batch reactor. The production of 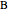 proceeds in cycles, each cycle being composed of a reaction period (time
proceeds in cycles, each cycle being composed of a reaction period (time  ) and a dead time
) and a dead time  . The dead time entails preparation of the reaction mixture before the reaction begins (filling the reactor and heating the mixture to the desired temperature, etc.) and preparation of the reactor for the next reaction period after the reaction time
. The dead time entails preparation of the reaction mixture before the reaction begins (filling the reactor and heating the mixture to the desired temperature, etc.) and preparation of the reactor for the next reaction period after the reaction time  (cooling of the reaction mixture to stop the reaction, emptying the reactor, and cleaning the reactor).
(cooling of the reaction mixture to stop the reaction, emptying the reactor, and cleaning the reactor).
Contributed by: Housam Binous and Ahmed Bellagi (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation