Orthonormal Polynomials under Different Inner Product Measures

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
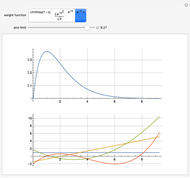
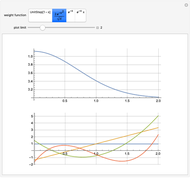
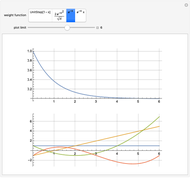
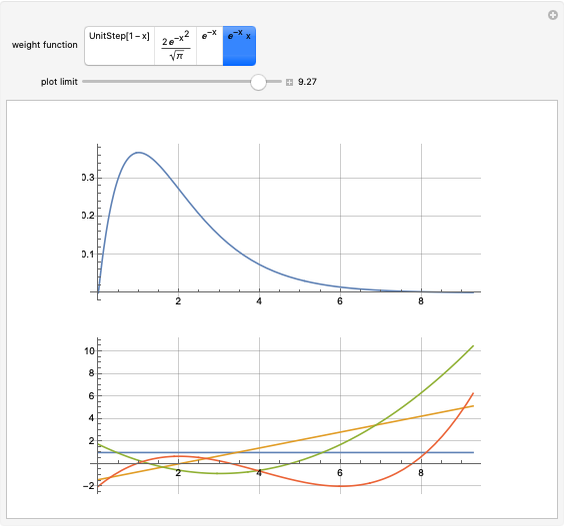
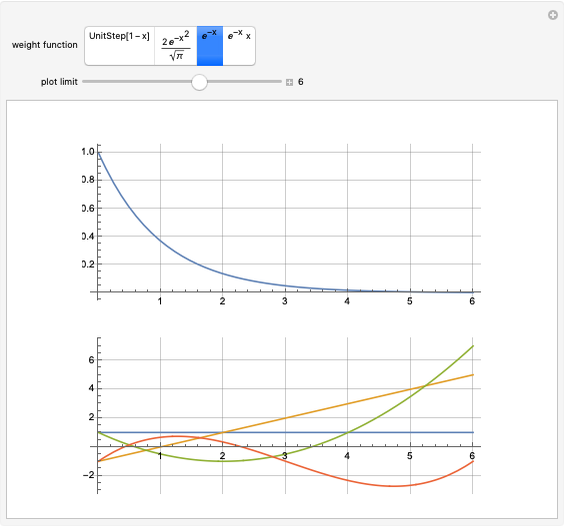
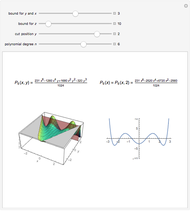
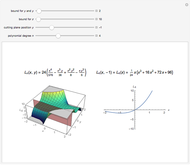
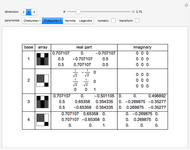
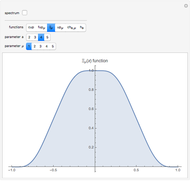
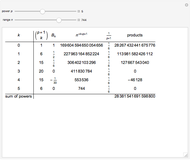
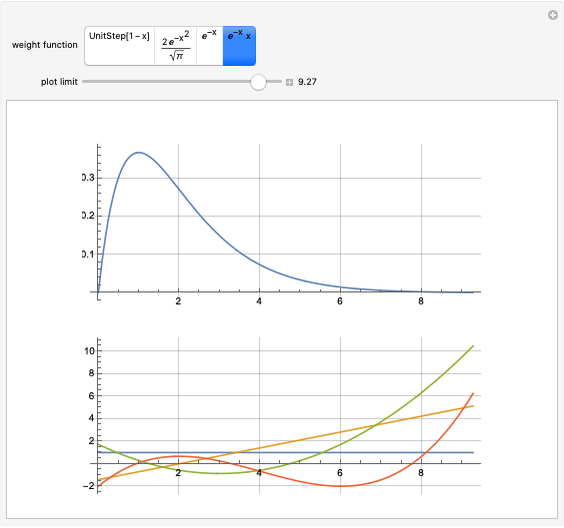
This Demonstration shows how the orthonormal polynomials of a space where the inner product is a weighted integral vary with the weight function  ,
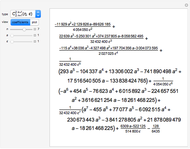
,  . Here, the monomial basis
. Here, the monomial basis  is orthonormalized by the Gram–Schmidt process with respect to the inner product
is orthonormalized by the Gram–Schmidt process with respect to the inner product 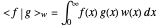 and the weight functions are probability measures (so that
and the weight functions are probability measures (so that  ) corresponding to the Legendre, Hermite, Laguerre and generalized Laguerre polynomials.
) corresponding to the Legendre, Hermite, Laguerre and generalized Laguerre polynomials.
Contributed by: Celestine Preetham Lawrence (August 2022)
Open content licensed under CC BY-NC-SA
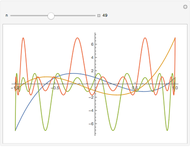
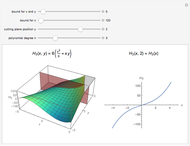
Snapshots
Details
The variable  is often time [1].
is often time [1].
Reference
[1] A. Gu, T. Dao, S. Ermon, A. Rudra and C. Re, "Hippo: Recurrent Memory with Optimal Polynomial Projections," Advances in Neural Information Processing Systems, 33, 2020 pp. 1474–1487. par.nsf.gov/biblio/10214620.
Permanent Citation