Spherical Harmonic on Constant Latitude or Longitude

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
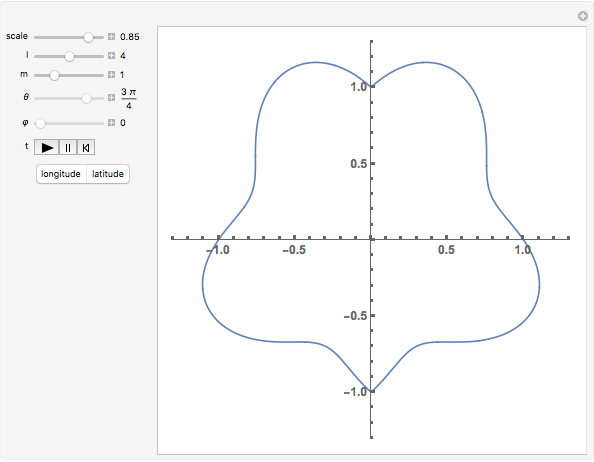
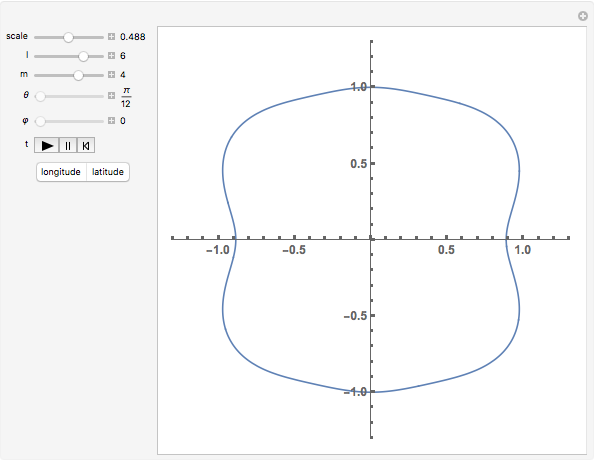
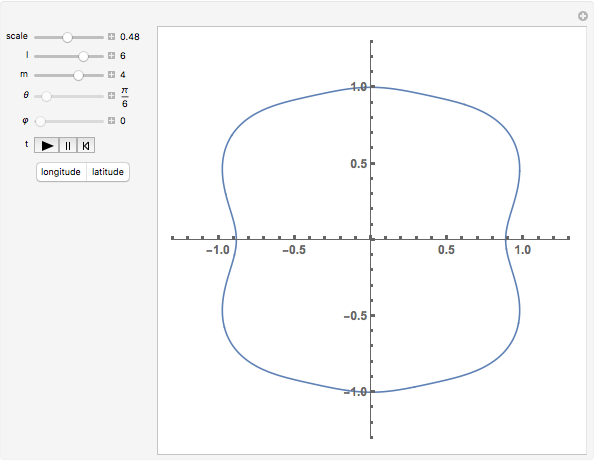
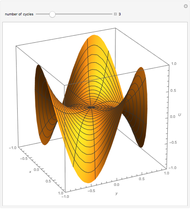
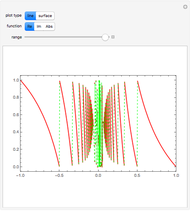
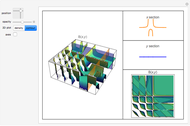
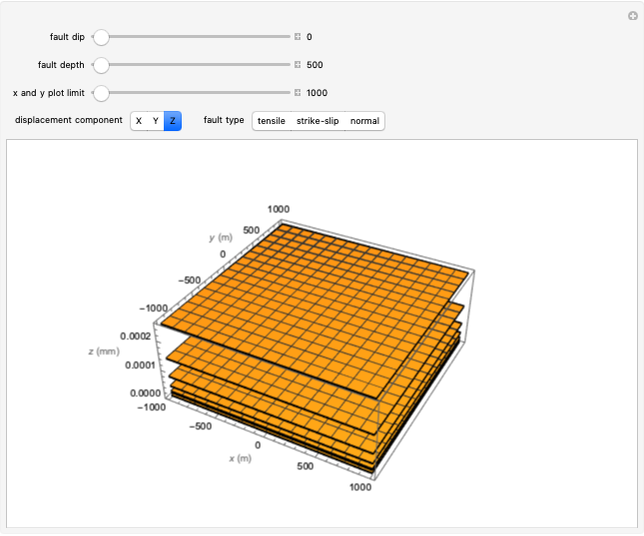
View the oscillating radial amplitude of the spherical harmonic (relative to the radial offset of 1.0) on a horizontal plane taken at constant latitude or on a vertical plane taken at constant longitude. You can set the degree and order of the harmonic ({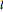 ,
, 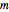 } with
} with 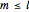 ), the latitude (
), the latitude ( ) when the "latitude" button is selected, or the longitude (
) when the "latitude" button is selected, or the longitude (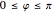 ) when the "longitude" button is selected. The relative amplitude (0 to 1) of the harmonic, when added to the constant radial offset of 1.0, is controlled by the slider labeled "scale". Use the "
) when the "longitude" button is selected. The relative amplitude (0 to 1) of the harmonic, when added to the constant radial offset of 1.0, is controlled by the slider labeled "scale". Use the " " control to change the oscillation speed, to start or stop it.
" control to change the oscillation speed, to start or stop it.
Contributed by: David von Seggern (University of Nevada) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Spherical harmonics (normalized) in the radial direction are expressed by the equation:
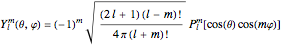 ,
,
where 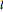 and
and 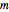 are the degree and order, respectively, of the generalized Legendre function
are the degree and order, respectively, of the generalized Legendre function 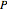 . The function is expressed on a sphere with polar angle
. The function is expressed on a sphere with polar angle  (starting from 0 at the positive
(starting from 0 at the positive  axis) and azimuth
axis) and azimuth  (counterclockwise from the
(counterclockwise from the  axis in the equatorial plane as viewed from the positive
axis in the equatorial plane as viewed from the positive  axis).
axis).
For display purposes in this Demonstration, 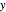 is multiplied by the time function
is multiplied by the time function 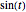 , scaled by a constant [0,1] and then added to 1.0. The radial motion in a plane given by constant
, scaled by a constant [0,1] and then added to 1.0. The radial motion in a plane given by constant  or
or  is then shown as a function of time, with a complete oscillation every
is then shown as a function of time, with a complete oscillation every 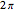 units of time.
units of time.
There are three common classes of radial spherical harmonics. The first, zonal harmonics of degree 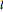 , is given when
, is given when  . For this class, there is no longitudinal variation and there are zeros along
. For this class, there is no longitudinal variation and there are zeros along 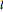 parallels of latitude. The second, sectoral harmonics of degree
parallels of latitude. The second, sectoral harmonics of degree 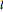 and order
and order 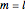 , has no latitudinal zeros but has zeros along
, has no latitudinal zeros but has zeros along 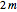 longitudes. The third, tesseral harmonics of degree
longitudes. The third, tesseral harmonics of degree 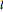 and order
and order 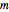 (
(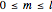 ), has zeros along
), has zeros along 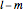 parallels of latitude and zeros along
parallels of latitude and zeros along 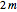 longitudes.
longitudes.
Permanent Citation