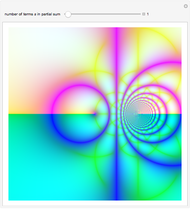
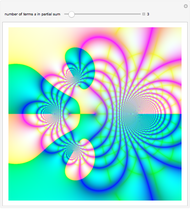
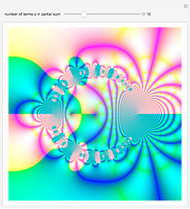
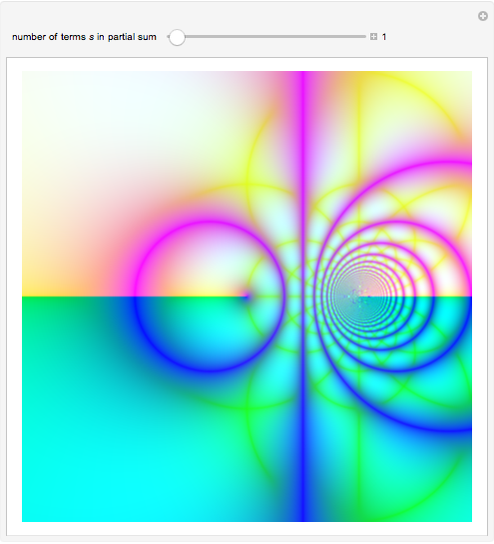
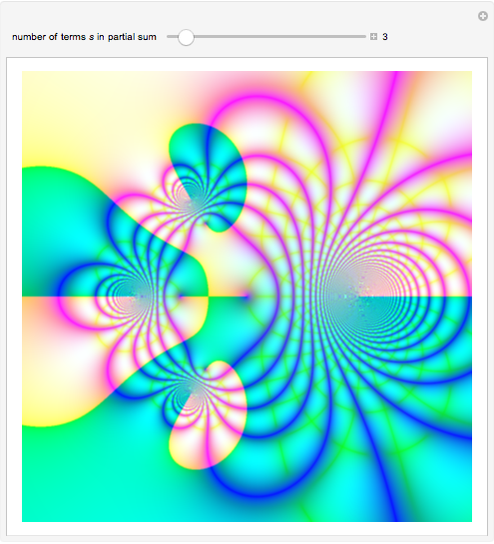
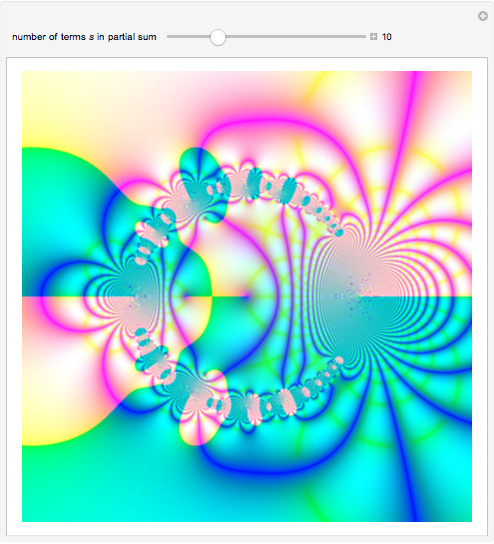
Partial Sums of a Lambert Series

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
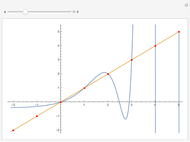
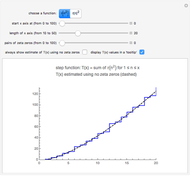
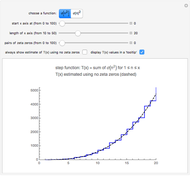
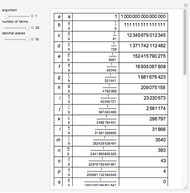
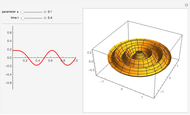
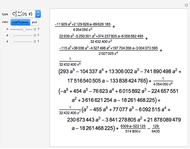
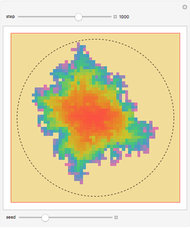
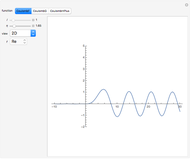
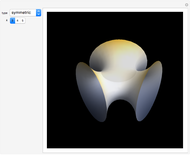
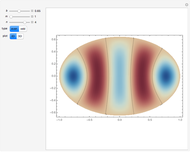
A Lambert series has the form  . For bounded coefficients
. For bounded coefficients  , the series converges in the unit disk and most poles lie on the unit circle. These series play an important role in analytic number theory and are related to the divisor function, Jacobi theta functions, the Möbius function, Euler's totient function, the Liouville function, the Ramanujan theta function, and the Riemann zeta function.
, the series converges in the unit disk and most poles lie on the unit circle. These series play an important role in analytic number theory and are related to the divisor function, Jacobi theta functions, the Möbius function, Euler's totient function, the Liouville function, the Ramanujan theta function, and the Riemann zeta function.
Contributed by: Enrique Zeleny (February 2015)
Based on a program by: Simon Woods
Open content licensed under CC BY-NC-SA
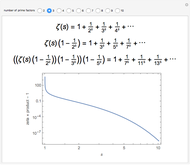
Snapshots
Details
References
[1] E. Wegert, Visual Complex Functions: An Introduction with Phase Portraits, New York: Birkhäuser, 2012.
[2] Mr. Wizard. "How can I generate this "domain coloring” plot?" Mathematica StackExchange. (Feb 5, 2015) mathematica.stackexchange.com/questions/7275/how-can-i-generate-this-domain-coloring-plot.
[3] J. Arndt, "On Computing the Generalized Lambert Series." arxiv.org/abs/1202.6525.
Permanent Citation