Phase Space of a Simple Pendulum

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
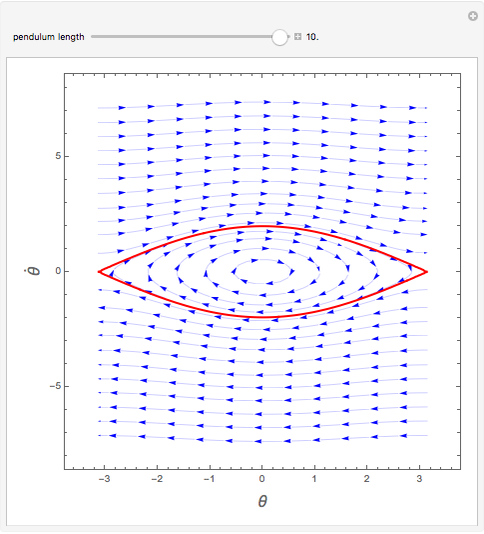
Consider the motion of a pendulum of length  described by the differential equation
described by the differential equation  , where
, where  is the gravitational acceleration and
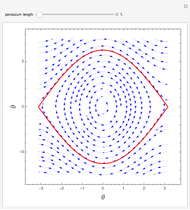
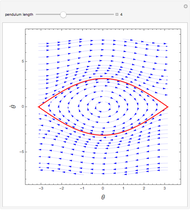
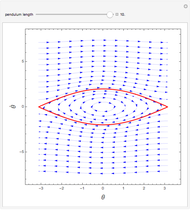
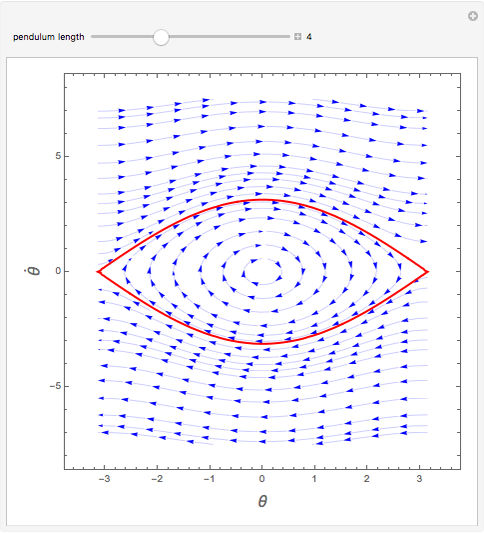
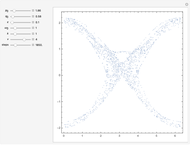
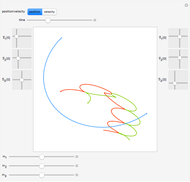
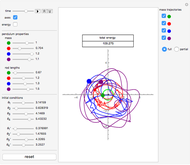
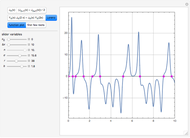
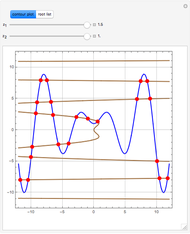
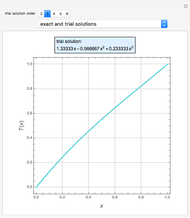
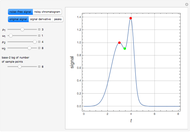
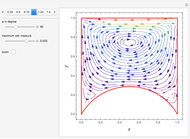
is the gravitational acceleration and  is the angle between the pendulum and the vertical direction. This Demonstration plots the phase space diagram (i.e.,
is the angle between the pendulum and the vertical direction. This Demonstration plots the phase space diagram (i.e.,  along the horizontal axis and
along the horizontal axis and  on the vertical axis). The separatrix, plotted in red, is given by
on the vertical axis). The separatrix, plotted in red, is given by  , where
, where  is the Hamiltonian of the system. The separatrix separates phase space into two different regions. The inside region, where the pendulum oscillates back and forth, corresponds to
is the Hamiltonian of the system. The separatrix separates phase space into two different regions. The inside region, where the pendulum oscillates back and forth, corresponds to  . The outside region corresponds to
. The outside region corresponds to  , where the pendulum continuously turns through vertical planar circles.
, where the pendulum continuously turns through vertical planar circles.
Contributed by: Housam Binous, Ahmed Bellagi, and Brian G. Higgins (October 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Phase Space of a Simple Pendulum"
http://demonstrations.wolfram.com/PhaseSpaceOfASimplePendulum/
Wolfram Demonstrations Project
Published: October 4 2013