Probability of a Union by the Principle of Inclusion-Exclusion

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
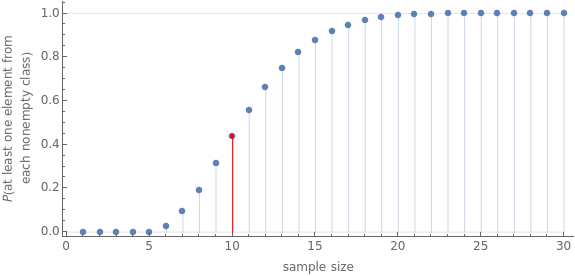
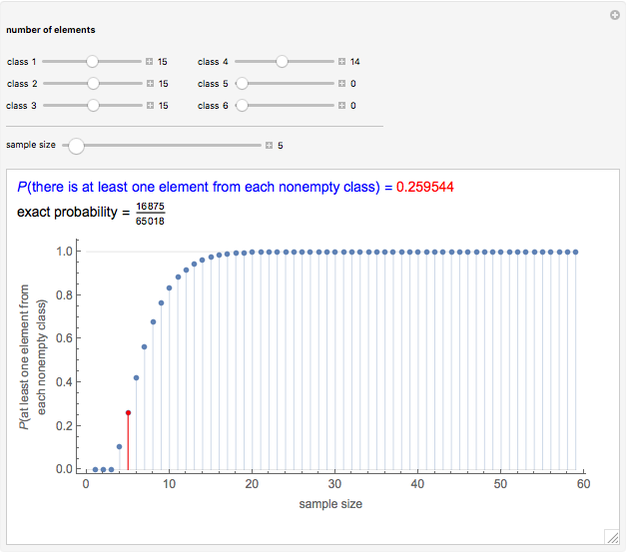
This Demonstration calculates the probability that there is at least one element from each of at most six classes when a given number of elements is sampled without replacement from among all the elements. This probability can be expressed in terms of the probability of a union of events and is calculated using the principle of inclusion-exclusion.
Contributed by: Heikki Ruskeepää (April 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
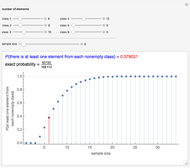
Snapshot 1: This is an example from [1, p. 73]; the same example is also considered in [2, p. 237]. We have six professors, six associate professors, 10 assistant professors, and 12 instructors; the total number of people is 34. A committee of size six is formed randomly. What is the probability that there is at least one person from each rank on the committee? Snapshot 1 shows that the probability is 0.379031 or, as an exact number, 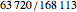 .
.
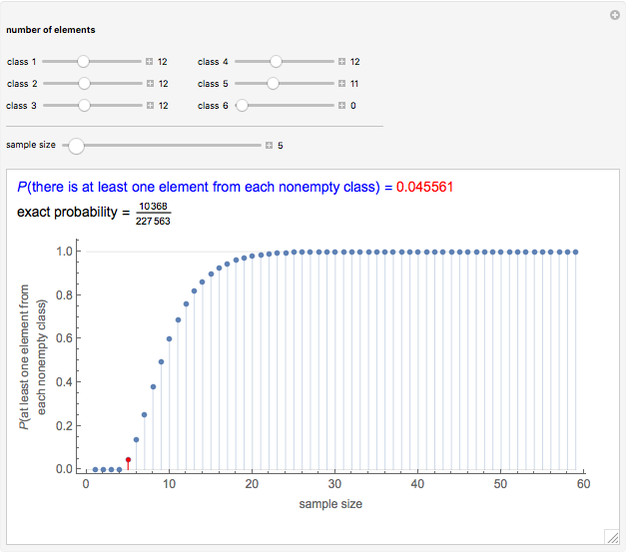
Snapshot 2: In a lottery in the USA, five numbers are drawn from the numbers 1 to 59. What is the probability that one number is drawn from each of the five sets 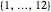 ,
, 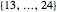 ,
, 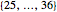 ,
, 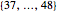 , and
, and 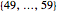 ? (Each of these sets contains 12 numbers, except the last one that contains 11 numbers.) The probability is only 0.04556. If we choose only 1, 2, 3, or 4 random numbers, the probability that one number is drawn from each of the five sets is, naturally, zero. If we choose 40 random numbers, the probability that one number is drawn from each of the five sets is, to six decimal places, 1.0, but the exact probability shows that the probability becomes exactly 1 only if we choose 49 or more numbers. Indeed, the 48 numbers 1 to 48 can be drawn from the first four sets, but among 49 numbers, there must be some in each of the five sets.
? (Each of these sets contains 12 numbers, except the last one that contains 11 numbers.) The probability is only 0.04556. If we choose only 1, 2, 3, or 4 random numbers, the probability that one number is drawn from each of the five sets is, naturally, zero. If we choose 40 random numbers, the probability that one number is drawn from each of the five sets is, to six decimal places, 1.0, but the exact probability shows that the probability becomes exactly 1 only if we choose 49 or more numbers. Indeed, the 48 numbers 1 to 48 can be drawn from the first four sets, but among 49 numbers, there must be some in each of the five sets.
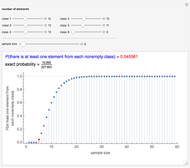
Snapshot 3: In the lottery of Snapshot 2, what is the probability that at least one number is drawn from each of the four sets 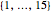 ,
, 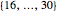 ,
, 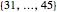 , and
, and 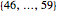 ? (These sets contain 15, 15, 15, and 14 numbers, respectively.) The probability is 0.2595.
? (These sets contain 15, 15, 15, and 14 numbers, respectively.) The probability is 0.2595.
Snapshot 4: In the same lottery, what is the probability that at least one number is drawn from each of the three sets  ,
, 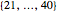 , and
, and 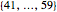 ? (These sets contain 20, 20, and 19 numbers, respectively.) The probability is 0.6471.
? (These sets contain 20, 20, and 19 numbers, respectively.) The probability is 0.6471.
Snapshot 5: Again in the same lottery, what is the probability that at least one number is drawn from each of the two sets  and
and  ? (These sets contain 30 and 29 numbers, respectively.) The probability is 0.9478. The probability is the same if the two sets are, say,
? (These sets contain 30 and 29 numbers, respectively.) The probability is 0.9478. The probability is the same if the two sets are, say, 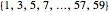 and
and 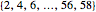 . (These sets also contain 30 and 29 numbers, respectively).
. (These sets also contain 30 and 29 numbers, respectively).
In this Demonstration, we have elements in at most six classes. We take a given number of elements at random without replacement from among all of the elements. What is the probability that we get at least one element from each class? Let  be the event that we get at least one element from class
be the event that we get at least one element from class  . We want to calculate
. We want to calculate 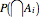 . By de Morgan's law, this probability can also be written as
. By de Morgan's law, this probability can also be written as 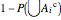 . Thus, we arrive at the probability of a union, where
. Thus, we arrive at the probability of a union, where 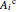 is the complement of
is the complement of  , that is,
, that is, 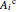 is the event that we get no elements from class
is the event that we get no elements from class  .
.
The probability of a union can be calculated by using the principle of inclusion-exclusion. For example,
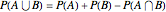 ,
,
 ,
,
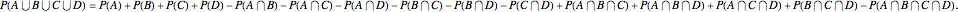
In sampling without replacement, the probabilities in these formulas can easily be calculated by binomial coefficients. In the example of Snapshot 1, we have to use the third formula above. The probability that we get no professors is  , the probability that we get no professors and no associate professors is
, the probability that we get no professors and no associate professors is 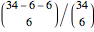 , the probability that we get no professors, no associate professors, and no assistant professors is
, the probability that we get no professors, no associate professors, and no assistant professors is 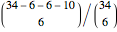 , and so on.
, and so on.
References
[1] S. Ghahramani, Fundamentals of Probability with Stochastic Processes, 3rd ed., Upper Saddle River, NJ: Pearson, 2005.
[2] P. J. Nahin, Digital Dice: Computational Solutions to Practical Probability Problems, Princeton, NJ: Princeton University Press, 2008.
Permanent Citation