Quantum State Discrimination with Two Qubits

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
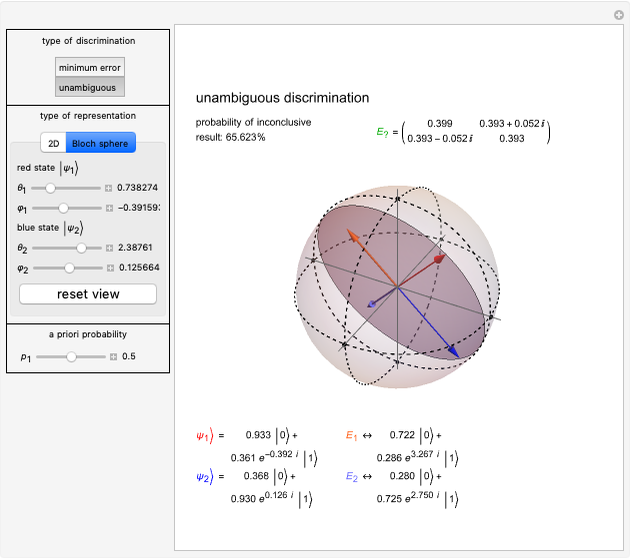
This Demonstration considers quantum-state discrimination for a system of two two-dimensional quantum states, as represented by two qubits. Two well-known techniques are employed: minimum-error discrimination and unambiguous discrimination.
Contributed by: Jaroslav Kysela (August 2022)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In quantum mechanics, states of physical systems are described by unit vectors in Hilbert space. A measurement on a physical system is described by a set of operators. In the standard approach, these operators are orthogonal projectors that sum to the identity. In a more general approach, which is referred to as positive operator-valued measure (POVM), a measurement is described by a set of positive semidefinite operators that sum to the identity. Imagine a situation in which an experimenter observes a physical system, which can be in one of two possible states, with the goal of finding out which state the system occupies. If the corresponding state vectors are orthogonal, you can always construct a measurement with two possible outcomes that unambiguously identifies the given state. This measurement consists of two projectors, one onto each state. When the two states are not orthogonal, perfect identification is not possible. However, a number of alternative techniques exist, to distinguish the two states as well as possible. Two well-known methods are "minimum-error state discrimination" and "unambiguous state discrimination" [1, 2].
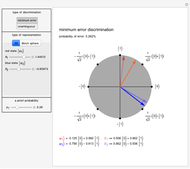
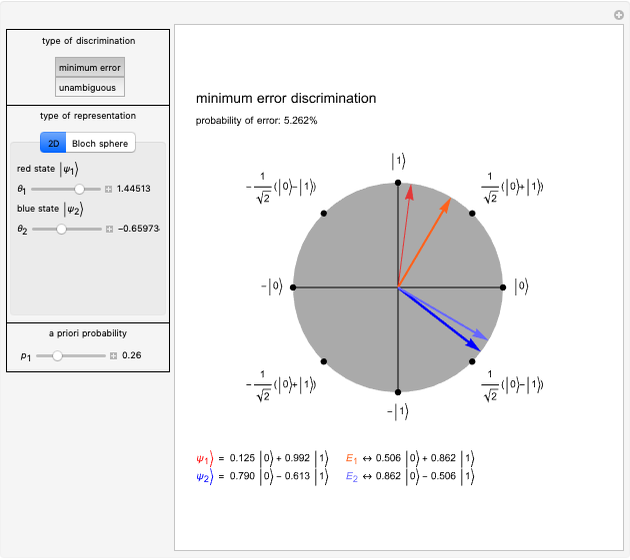
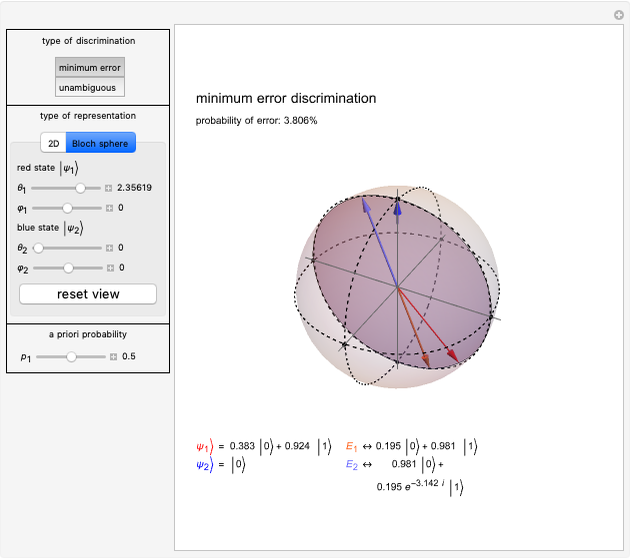
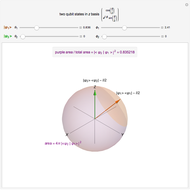
Minimum-error state discrimination is a standard projective measurement that has minimum probability of an erroneous identification of a state. In this Demonstration, you can adjust the form of two two-dimensional quantum states ψ1Ket and ψ2Ket that are to be distinguished. They are represented by red and blue arrows, respectively. The projector 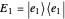 (
(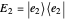 ) that identifies state
) that identifies state 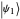 (ψ2Ket) is shown as a light-blue vector
(ψ2Ket) is shown as a light-blue vector 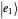 (light-red vector
(light-red vector  ). Since the overlap between
). Since the overlap between 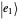 and ψ1Ket (
and ψ1Ket (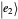 and ψ2Ket) is not perfect, there is a nonzero probability of error [3]. When the red and blue vectors correspond to the same state, no discrimination is possible, in which case the background turns orange and all values read "N/A".
and ψ2Ket) is not perfect, there is a nonzero probability of error [3]. When the red and blue vectors correspond to the same state, no discrimination is possible, in which case the background turns orange and all values read "N/A".
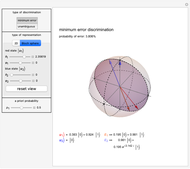
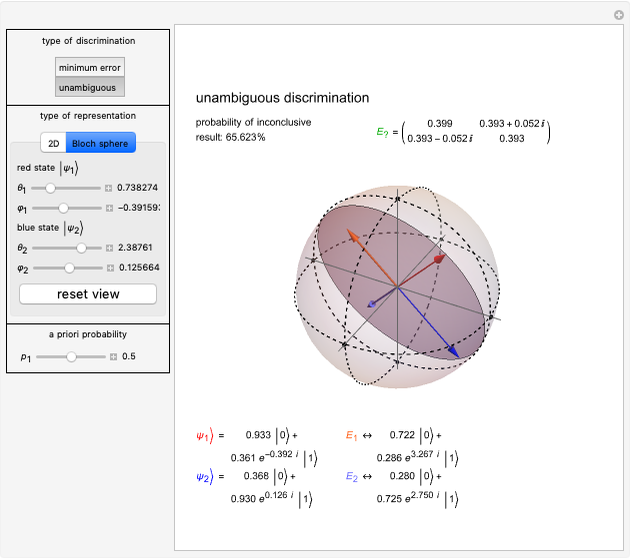
The unambiguous state discrimination is an example of a POVM measurement, which has three, rather than two, possible outcomes [4]. The first outcome is associated with the operator 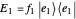 , which unambiguously identifies state ψ1Ket, depicted as a non-normalized light red vector
, which unambiguously identifies state ψ1Ket, depicted as a non-normalized light red vector 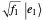 . Analogously, the second outcome is associated with the operator
. Analogously, the second outcome is associated with the operator 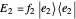 , which unambiguously identifies state ψ2Ket, depicted as a non-normalized light blue vector
, which unambiguously identifies state ψ2Ket, depicted as a non-normalized light blue vector  . The price for unambiguous identification is the existence of the third outcome, which is associated with the green operator
. The price for unambiguous identification is the existence of the third outcome, which is associated with the green operator 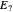 and which corresponds to an inconclusive result that contains no information about the state of the measured system. The corresponding POVM may not exist for some parameter regimes, in which case the background turns orange and values read "N/A".
and which corresponds to an inconclusive result that contains no information about the state of the measured system. The corresponding POVM may not exist for some parameter regimes, in which case the background turns orange and values read "N/A".
The efficiency of the state discrimination also depends on the probability with which the measured system is prepared in state ψ1Ket or ψ2Ket. In the extreme case, when the probability of the system being in state ψ2Ket is zero, no discrimination is necessary, as ψ1Ket is the only state that appears. In a general case, the probability of the system being in state ψ1Ket prior to the measurement is given by  and is referred to as the a priori probability. The optimal choice of measurement operators depends on this probability. In this Demonstration, the thickness and opacity of red and blue vectors change according to their a priori probabilities.
and is referred to as the a priori probability. The optimal choice of measurement operators depends on this probability. In this Demonstration, the thickness and opacity of red and blue vectors change according to their a priori probabilities.
The two methods of quantum state discrimination are illustrated in two (inequivalent and independent) representations of quantum states. The "2D" representation depicts states as two-dimensional vectors in a plane. Physically relevant are only states in the above right quadrant corresponding to  , but for consistency, the range is extended to a full circle with
, but for consistency, the range is extended to a full circle with  , such that
, such that  (and analogously for
(and analogously for 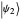 ). Two states are orthogonal in the two-dimensional Hilbert space if their vectors are orthogonal, that is,
). Two states are orthogonal in the two-dimensional Hilbert space if their vectors are orthogonal, that is,  . The two-dimensional quantum states can be represented by points on a Bloch sphere, in which each unit vector is parametrized by two angles
. The two-dimensional quantum states can be represented by points on a Bloch sphere, in which each unit vector is parametrized by two angles  and
and 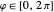 , such that
, such that 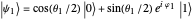 (and analogously for
(and analogously for  ). In this representation, two quantum states are orthogonal if their vectors are antiparallel, that is,
). In this representation, two quantum states are orthogonal if their vectors are antiparallel, that is, 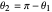 and
and 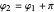 . The three-dimensional graphics can be rotated and the viewpoint can be reset by clicking "reset view".
. The three-dimensional graphics can be rotated and the viewpoint can be reset by clicking "reset view".
References
[1] S. M. Barnett and S. Croke, "Quantum State Discrimination," Advances in Optics and Photonics, 1(2), 2009 pp. 238–278. doi:10.1364/AOP.1.000238.
[2] J. A. Bergou, U. Herzog and M. Hillery, "Discrimination of Quantum States," Quantum State Estimation (M. Paris and J. Rveháček, eds.) Heidelberg: Springer, 2004 pp. 417–465. doi:10.1007/978-3-540-44481-7_11.
[3] C. W. Helstrom, Quantum Detection and Estimation Theory, New York: Academic Press, 1976.
[4] I. D. Ivanovic, "How to Differentiate between Non-orthogonal States," Physics Letters A, 123(6), 1987 pp. 257–259. doi:10.1016/0375-9601(87)90222-2.
Permanent Citation