Renormalization of Curlicue Fractals

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Given a positive integer  and a real number
and a real number  in the interval
in the interval 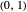 , consider the polygonal path in the plane starting at the origin, followed by
, consider the polygonal path in the plane starting at the origin, followed by  steps of length 1 in directions
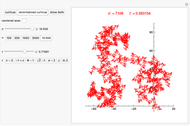
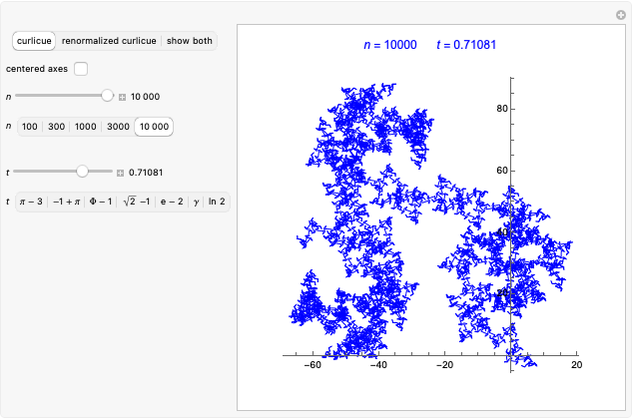
steps of length 1 in directions  , respectively. Such a path is called a curlicue or curlicue fractal, since it exhibits a fractal-like structure. Berry and Goldberg showed that a curlicue with parameter pair
, respectively. Such a path is called a curlicue or curlicue fractal, since it exhibits a fractal-like structure. Berry and Goldberg showed that a curlicue with parameter pair  is (up to scaling and rotation/reflection) similar to a curlicue with parameter pair
is (up to scaling and rotation/reflection) similar to a curlicue with parameter pair 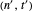 , where
, where 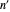 and
and  are given by
are given by 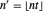 and
and 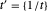 if
if  is even,
is even, 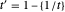 if
if 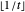 is odd. Here
is odd. Here 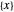 denotes the fractional part of
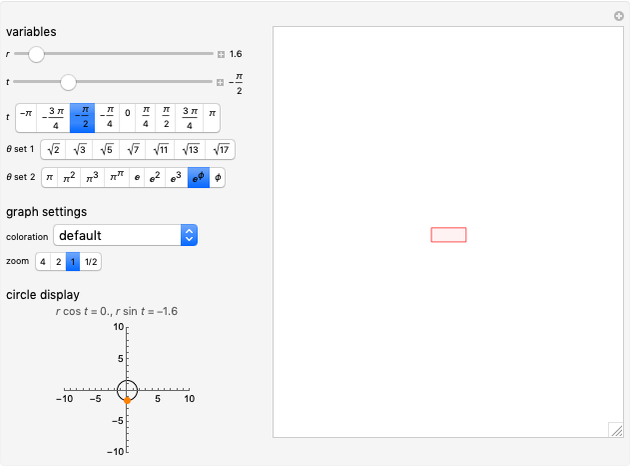
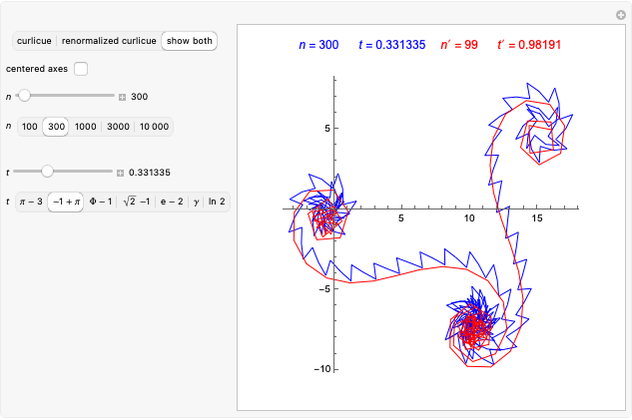
denotes the fractional part of 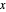 . Transformation of the former curlicue into the latter is called renormalization. It is of considerable interest, since it can rigorously prove some geometric features of curlicues. This Demonstration illustrates the renormalization process by showing the original and renormalized curlicues for a wide range of parameters
. Transformation of the former curlicue into the latter is called renormalization. It is of considerable interest, since it can rigorously prove some geometric features of curlicues. This Demonstration illustrates the renormalization process by showing the original and renormalized curlicues for a wide range of parameters 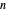 and
and  .
.
Contributed by: Tri Do, Kevin Liu and A. J. Hildebrand (August 27)
(Based on an undergraduate research project at the Illinois Geometry Lab in Fall 2022)
Open content licensed under CC BY-NC-SA
Details
A curlicue with parameters 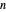 and
and  is the path in the complex plane obtained by connecting the partial sums of
is the path in the complex plane obtained by connecting the partial sums of
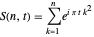 ,
,
or, equivalently, the polygonal path in the plane obtained by starting at the origin, followed by 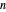 unit steps in directions
unit steps in directions 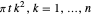 .
.
Assuming (without loss of generality) that  , Berry and Goldberg [1] showed that if
, Berry and Goldberg [1] showed that if 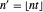 and, if
and, if  is even,
is even,  , otherwise
, otherwise 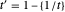 , then
, then
(1) 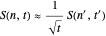 if
if 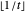 is odd
is odd
and
(2) 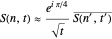 if
if 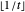 is even,
is even,
where  denotes the complex conjugate of
denotes the complex conjugate of  . The transformation given by (1) and (2) relates a curlicue with parameters
. The transformation given by (1) and (2) relates a curlicue with parameters 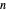 and
and  to a curlicue with parameters
to a curlicue with parameters  and
and  scaled by a factor
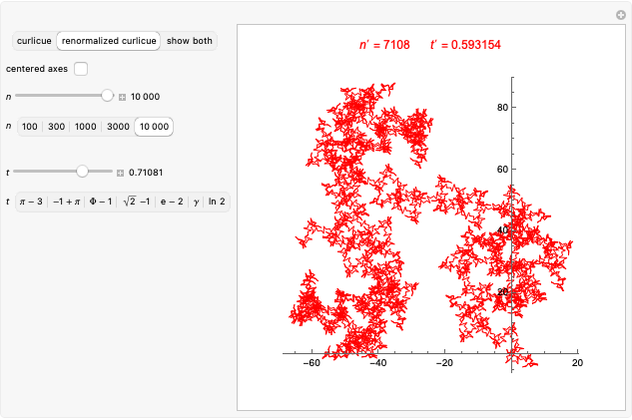
scaled by a factor  . This transformation is called the renormalization of the curlicue
. This transformation is called the renormalization of the curlicue  . This Demonstration illustrates the renormalization process by showing the curlicues on the left and right sides of (1) and (2) for all parameter pairs
. This Demonstration illustrates the renormalization process by showing the curlicues on the left and right sides of (1) and (2) for all parameter pairs 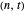 with
with  and
and 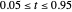 , as well as for a set of interesting predefined values of
, as well as for a set of interesting predefined values of 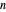 and
and  .
.
Reference
[1] M. V. Berry and J. Goldberg, "Renormalization of Curlicues," Nonlinearity, 1(1), 1988 pp. 1–26. doi:10.1088/0951-7715/1/1/001.
Snapshots
Permanent Citation