Wolfram Demonstrations Project

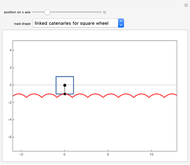
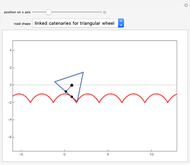
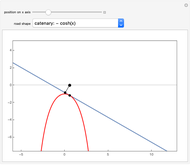
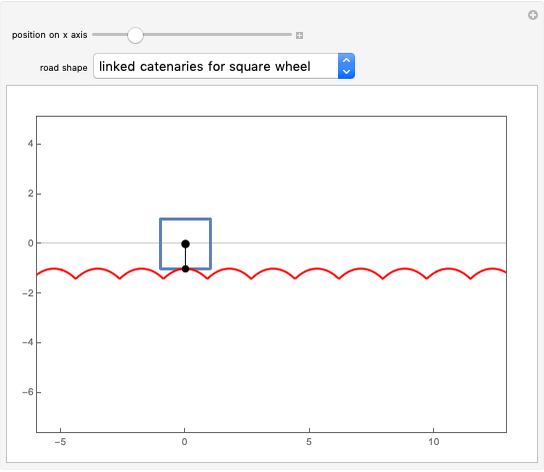
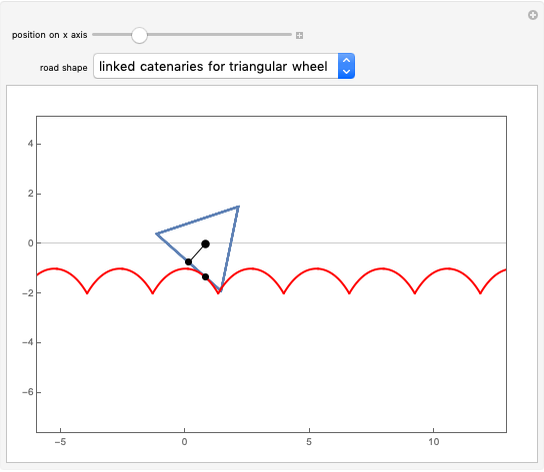
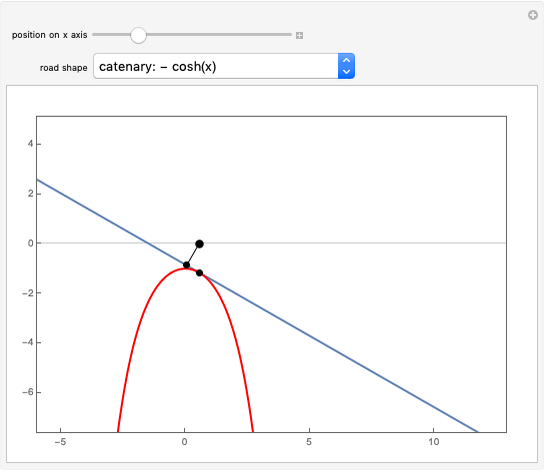
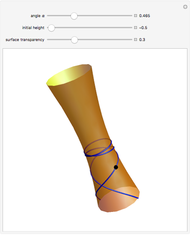
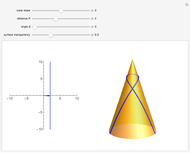
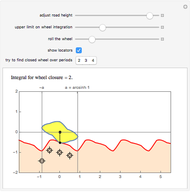
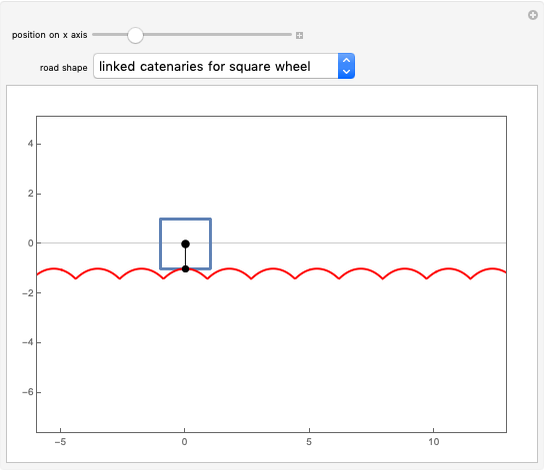
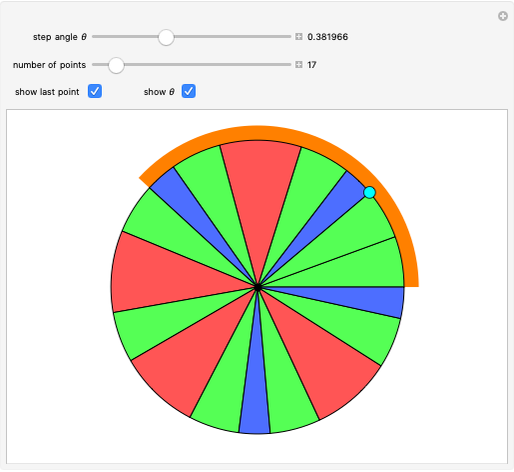
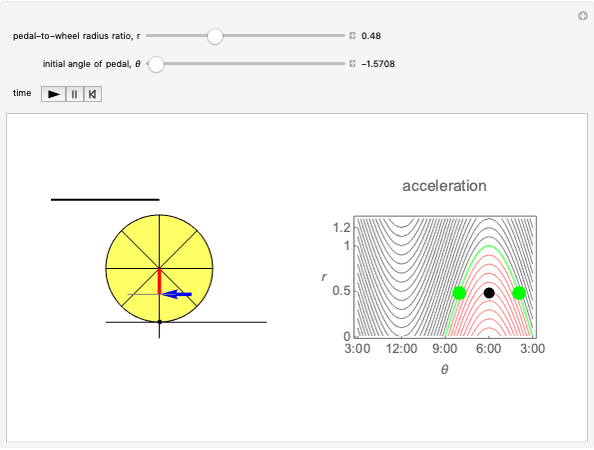
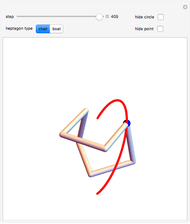
Given a road, one can solve a differential equation to get a wheel that will roll smoothly along the road in the sense that the center of the wheel does not move up or down. This Demonstration presents eight examples, the first being the famous one of a square wheel rolling on a series of linked catenaries. This example derives from the pure catenary case. The triangular case is of interest because the wheel actually crashes into the road before reaching the cusp. The parabola, given by

, is unusual in that the wheel is exactly congruent to the road. For a given road, the wheel will not necessarily close up; this is illustrated by the three cosine examples. When the standard cosine function has the distance of the road's top from the

axis as

, then the wheel closes up over

periods of the road. The cases of

and

are illustrated, as well as a cosine case where the wheel does not close up.

Contributed by: Stan Wagon (Macalester College, USA)

Slider Zoom

Given the road in the form

, the wheel is given in polar coordinates by

, where

is the solution to the differential equation

with

. The details were first worked out by James Clerk Maxwell in 1849 [1], though his work seems to have been forgotten. A detailed modern investigation was carried out by G. B. Robison (1960) [2], who rediscovered the result found by Maxwell that a straight line rolls smoothly on a catenary. The important idea of truncating the catenary and line so as to get a rolling square is due to D. G. Wilson (1964) [3]. Further details and examples can be found in the paper by Hall and Wagon [4]. A photo of a working square-wheel tricycle can be found at the author's website [5].

References

[1] J. C. Maxwell, "On the Theory of Rolling Curves," Transactions of the Royal Society of Edinburgh, 16(5), 1849 pp. 519–540 (p. 537, Ex. 12). archive.org/details/transactionsofro16roy/page/518/mode/2up.

[2] G. B. Robison, "Rockers and Rollers," Mathematics Magazine, 33(3), 1960 pp. 139–144. (Result first in E1033 1952.) www.jstor.org/stable/3029034?origin=crossref.

[3] D. G. Wilson, Problem E1668, American Mathematical Monthly, 71(2), 1964 p. 205. Solution: 72(1), 1965 pp. 82–83.

[4] L. Hall and S. Wagon, "Roads and Wheels," Mathematics Magazine, 65(5), 1992 pp. 283–301. doi.org/10.1080/0025570X .1992.11996043.

[5] S. Wagon. stanwagon.com.

Stan Wagon (Macalester College, USA)

"Roads and Wheels"
http://demonstrations.wolfram.com/RoadsAndWheels/
Wolfram Demonstrations Project
Published: May 4, 2022