Four-Coloring Planar Graphs

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
The famous four-color theorem, proved in 1976, says that the vertices of any planar graph can be colored in four colors so that adjacent vertices receive different colors. Kempe's method of 1879, despite falling short of being a proof, does lead to a good algorithm for four-coloring planar graphs. The method is recursive. One finds a vertex  that has degree at most 5; such exists by Euler's formula for graphs in the plane,
that has degree at most 5; such exists by Euler's formula for graphs in the plane,  , where
, where  ,
, 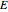 , and
, and 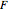 are the number of vertices, edges, and faces. Then assume the rest of the graph to be properly colored and color
are the number of vertices, edges, and faces. Then assume the rest of the graph to be properly colored and color  by considering three cases:
by considering three cases:
Contributed by: Stan Wagon (August 2010)
(Macalester College)
Open content licensed under CC BY-NC-SA
Snapshots
Details
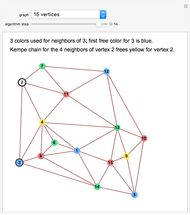
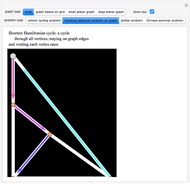
Snapshot 1. Kempe's method always works in the four-neighbor case. In this 15-vertex example the colors of vertices 4 and 6 can be switched (a yellow-green Kempe chain), which frees up yellow for use on 2.
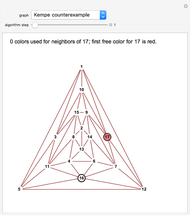
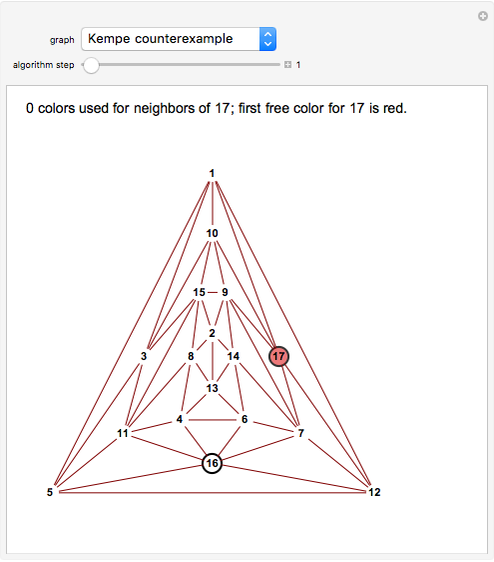
Snapshot 2. For the counterexample, Kempe's chains get tangled at the last step, when vertex 1 is to be colored. One tries to eliminate the green at 12 by switching green and yellow at 12 and 7; thus vertex 7 becomes green. Then the attempted elimination of the other green at 10 via a green/blue chain (10, 9, 7, 6, 13, 8, 11, 5) hits the newly colored green at 7 and continues through to 5, which ends up green, thus foiling the attempt.
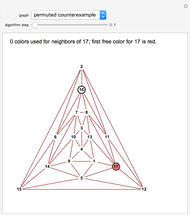
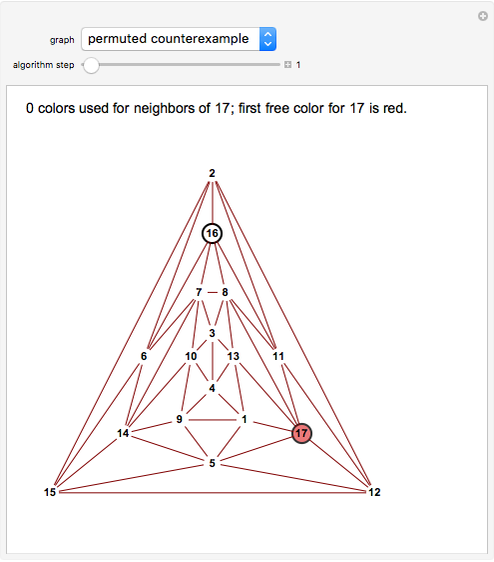
Snapshot 3. For this permutation of the bad example the last step again involves vertex 1, but now only three colors appear among its five neighbors so it gets colored green.
For complete details of the Kempe chain operation see [1] or [2]. The method always works when there are four neighbors of the current vertex. While the error in Kempe's method was discovered by P. J. Heawood in 1889, the first example of a graph that foils the algorithm was due to A. Errera in 1921.
While the success probability for permutations of the Errera graph is 90%, for the graph consisting of several disjoint copies of the Errera graph, this probability would quickly decrease. Thus one should use a more general method that combines Kempe's ideas with those of I. Kittell; see details in [2].
[1] J. P. Hutchinson and S. Wagon, "Kempe Revisited," American Mathematical Monthly, 105, (1998) pp. 170–174.
[2] S. Wagon, Mathematica in Action, 3rd ed., New York: Springer-Verlag, 2010.
Permanent Citation