Selective Fractalization of Chevron-Type Polygons Edges

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
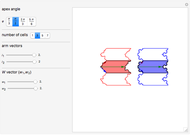
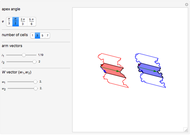
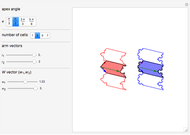
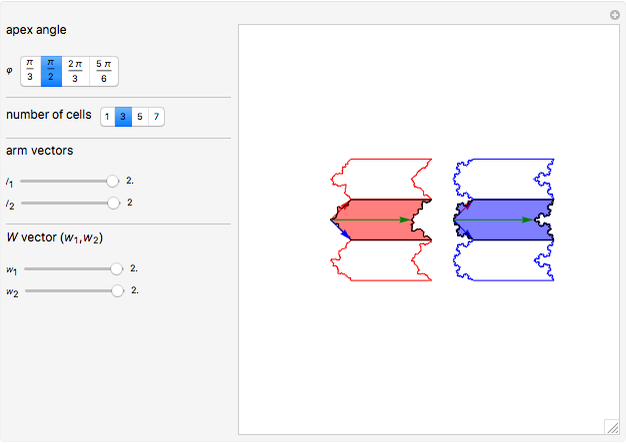
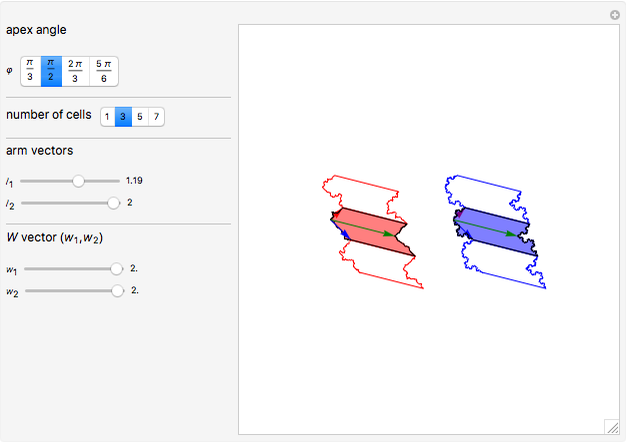
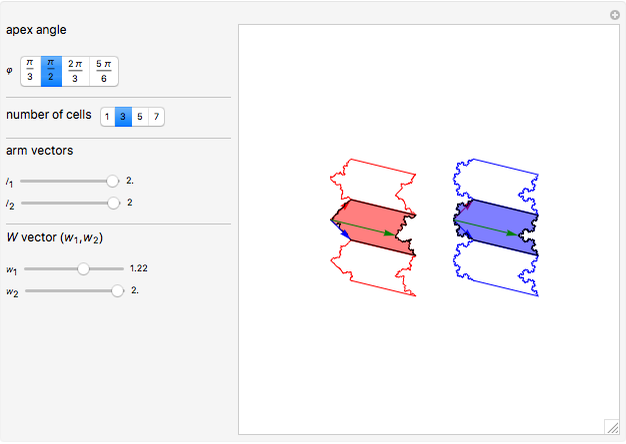
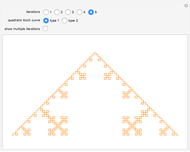
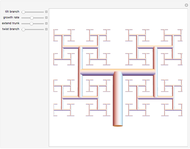
This Demonstration explores the fractalization of arbitrarily chosen edges of arbitrary polygons. A chevron-type concave polygon is used as a representative geometrical figure. The particular edges of this chevron-type polygon are fractalized with Koch curves. Then the copies of the resulting polygons are tiled and concatenated via straight non-fractalized edges so that they form elongated structures. Two types of fractalization are considered for comparison: randomized Koch curve (red, left) and regular Koch curve (blue, right).
Contributed by: Vasil Saroka (January 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
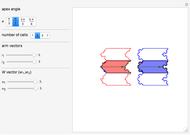
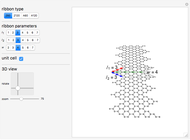
The chevron-type concave polygon is described by three vectors. Two-arm vectors are defined as
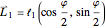 (red),
(red),
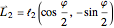 (blue),
(blue),
where  is the apex angle.
is the apex angle.
The third width vector is
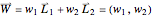 (green).
(green).
Snapshot 1: tiled chevron structure with symmetric arms  and symmetric width vector
and symmetric width vector 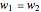
Snapshot 2: tiled chevron structure with asymmetric arms 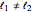 and symmetric width vector
and symmetric width vector 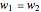
Snapshot 3: tiled chevron structure with symmetric arms  and asymmetric width vector
and asymmetric width vector 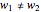
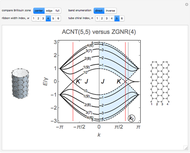
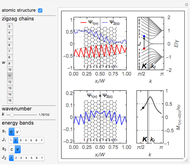
This model of the edge randomization by Koch curves can be applied to study the edge disorder in zigzag-shaped graphene nanoribbons [1] similar to what has been done for phosphorene quantum dots [2]. The shaded concave chevron-type polygon is a mathematical representation of the unit cell of zigzag-shaped graphene nanoribbon superlattices [1], which are also referred to in the literature as edge-modified zigzag-shaped ribbons [3] or jagged graphene nanoribbons [4].
References
[1] V. A. Saroka and K. G. Batrakov, "Zigzag-Shaped Superlattices on the Basis of Graphene Nanoribbons: Structure and Electronic Properties," Russian Physics Journal, 59(5), 2016 pp. 633–639. doi:10.1007/s11182-016-0816-6.
[2] V. A. Saroka, I. Lukyanchuk, M. E. Portnoi and H. Abdelsalam, "Electro-optical Properties of Phosphorene Quantum Dots," Physical Review B, 96(8), 2017 085436. doi:10.1103/PhysRevB.96.085436.
[3] V. A. Saroka, K. G. Batrakov and L. A. Chernozatonskii, "Edge-Modified Zigzag-Shaped Graphene Nanoribbons: Structure and Electronic Properties," Physics of the Solid State, 56(10), 2014 pp. 2135–2145. doi:10.1134/S106378341410028X.
[4] V. A. Saroka, K. G. Batrakov, V. A. Demin and L. A. Chernozatonskii, "Band Gaps in Jagged and Straight Graphene Nanoribbons Tunable by an External Electric Field," Journal of Physics: Condensed Matter, 27(14), 2015 145305. doi:10.1088/0953-8984/27/14/145305.
Permanent Citation