Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Solving the Secular Equation for Zigzag and Bearded Graphene Nanoribbons

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

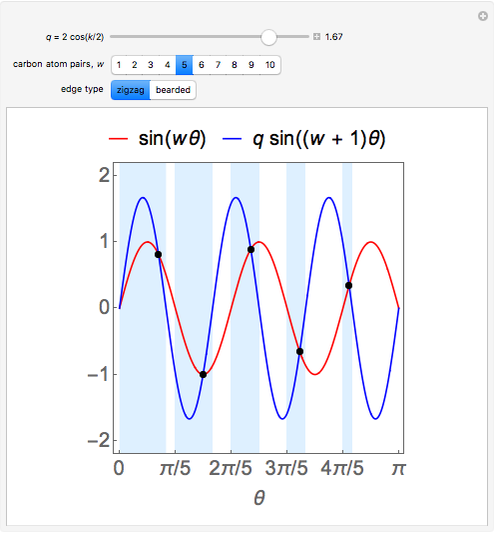
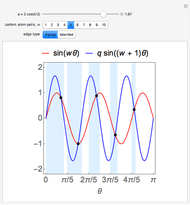
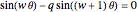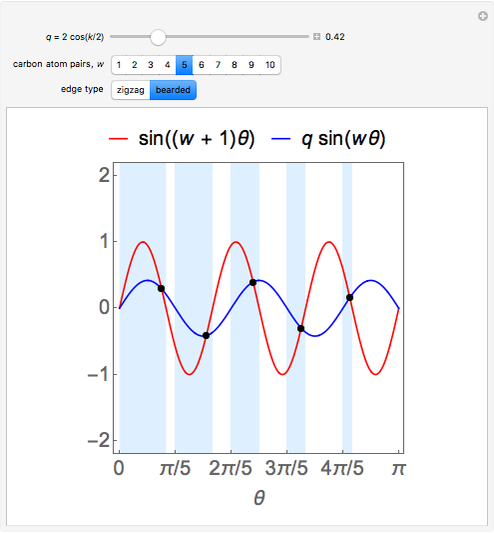
This Demonstration explores the solutions of the secular equations for graphene nanoribbons with zigzag and bearded edges. For graphene nanoribbons with zigzag edges, the secular equation is , while for a ribbon with bearded edges it is 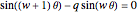. For ribbons containing 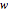pairs of carbon atoms in their unit cells, these equations quantize the transverse momentum of the electron, , and couple it to the longitudinal momentum, 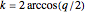. The equation for a ribbon with zigzag edges is the same as equation (19) in [1]. The equation for a ribbon with bearded edges, 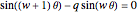, is different from the equation 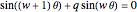given in reference [2]. The sign in front of the second term is of no physical importance, but the minus is more convenient for mathematical treatment, as has been discussed for zigzag ribbons [1].

Contributed by: Vasil Saroka (June 2017)
Open content licensed under CC BY-NC-SA

Snapshots

Details

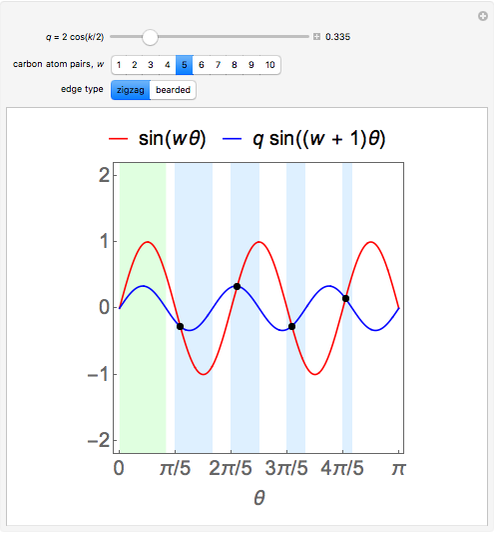
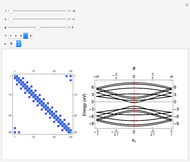
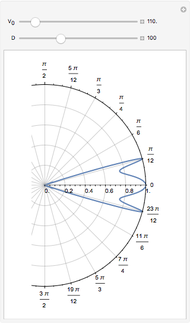
The lowest solutions of the secular equations disappear for 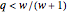and for 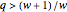in the case of a zigzag [1] and bearded [2] graphene nanoribbon, respectively.

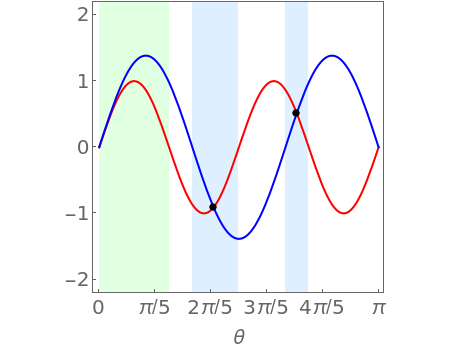
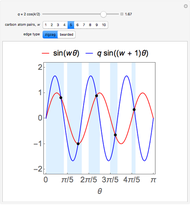
Snapshot 1: 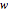solutions in light blue regions for a zigzag graphene nanoribbon

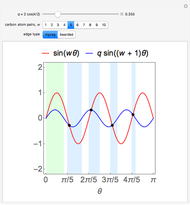
Snapshot 2: solutions in the light blue regions and one missing solution in the light green region for a zigzag graphene nanoribbon

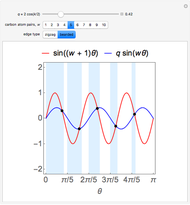
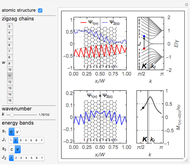
Snapshot 3: 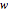solutions in the light blue regions for a bearded graphene nanoribbon

Snapshot 4: solutions in the light blue regions and one missing solution in the light green region for a bearded graphene nanoribbon

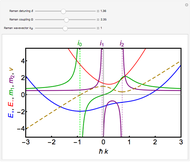
The missing solution restored by the analytical continuation 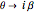gives rise to so-called edge states [2, 3]. The localization of the solutions 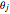within the light blue regions defines the parity of the electron wavefunction and, therefore, optical selection rules [1].

References

[1] V. A. Saroka, M. V. Shuba and M. E. Portnoi, "Optical Selection Rules of Zigzag Graphene Nanoribbons," Physical Review B, 95(15), 2017 155438. doi:10.1103/PhysRevB.95.155438.

[2] D. J. Klein, "Graphitic Polymer Strips with Edge States," Chemical Physics Letters, 217(3), 1994 pp. 261–265. doi:10.1016/0009-2614(93)E1378-T.

[3] M. Fujita, K. Wakabayashi, K. Nakada and K. Kusakabe, "Peculiar Localized State at Zigzag Graphite Edge," Journal of the Physical Society of Japan, 65(7), 1996 pp. 1920–1923. doi:10.1143/JPSJ.65.1920.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send