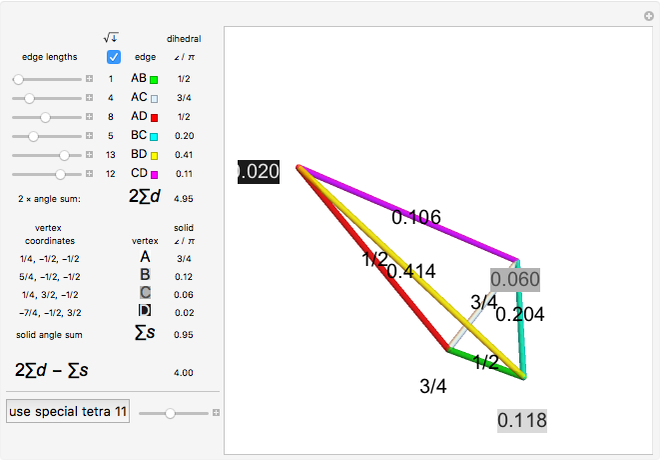
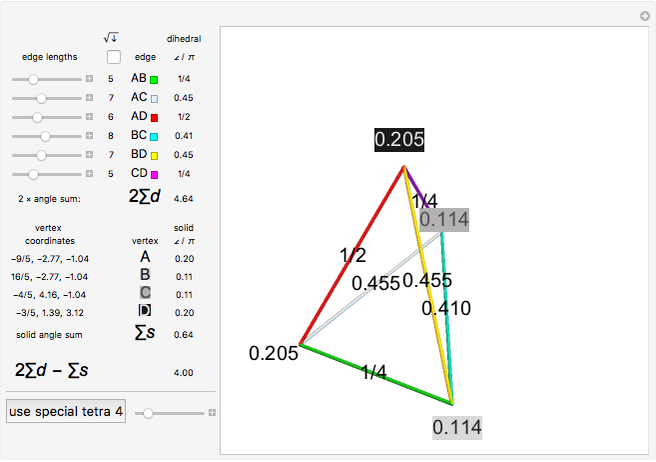
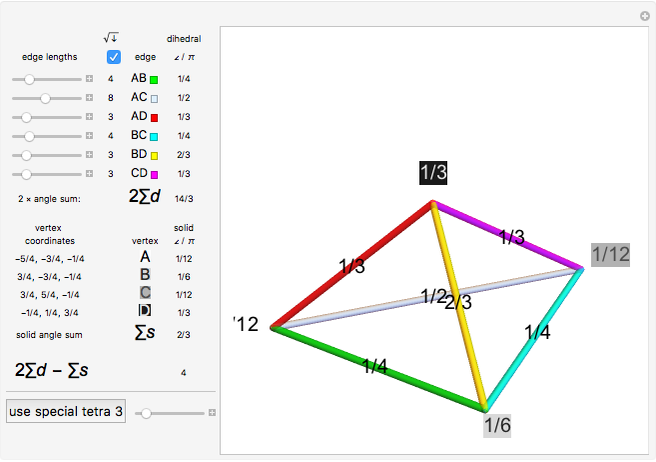
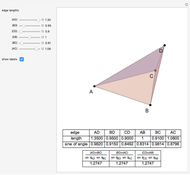
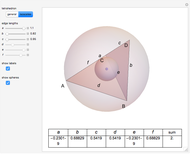
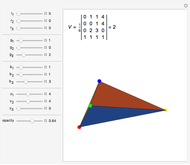
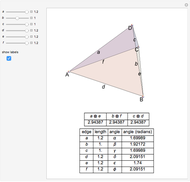
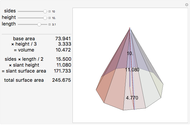
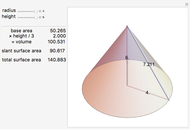
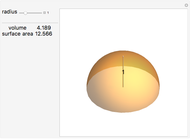
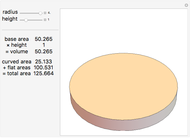
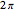Solid and Dihedral Angles of a Tetrahedron
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
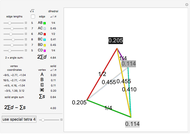
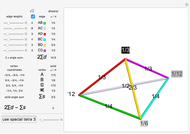
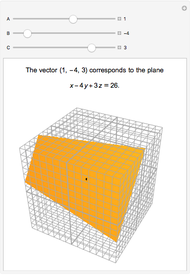
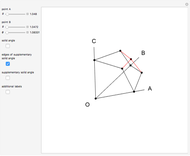
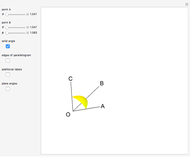
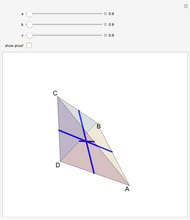
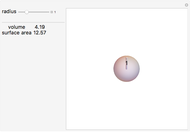
During an eclipse, the Moon and Sun appear to have roughly the same size viewed from Earth. The field of view of an object is called the solid angle. A unit sphere around the observer has a solid angle of  steradians, the same as the surface area.
steradians, the same as the surface area.
Contributed by: Ed Pegg Jr (July 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation