Space-Filling Tetrahedra

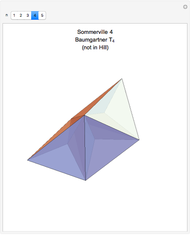
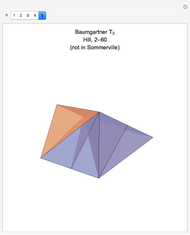
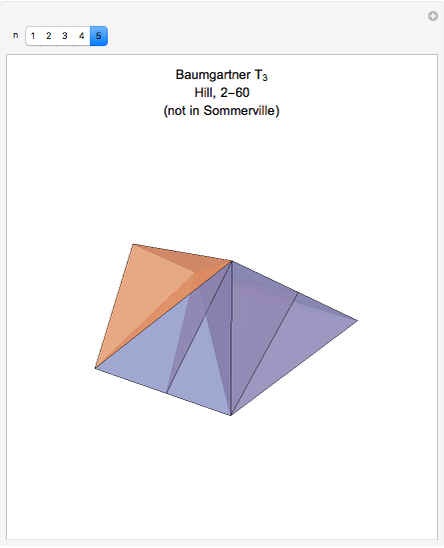
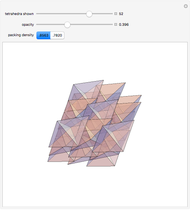
There are five known space-filling tetrahedra when mirror images are not allowed. Hill (1896), Baumgartner (1968), and Sommerville (1923) each enumerated four of the five.

Goldberg (1972) was the first to list all five. He also studied dissections of triangular prisms and found three basic ways in which a prism could be split into identical tetrahedra, if mirror images are allowed. Each of these three methods leads to infinite families of tetrahedra. All three methods are represented in the five tetrahedra listed here.

Whether other space-filling tetrahedra exist is a long unsolved question that dates back to Aristotle.