Solution of One-Dimensional Stefan Problem with Orthogonal Collocation
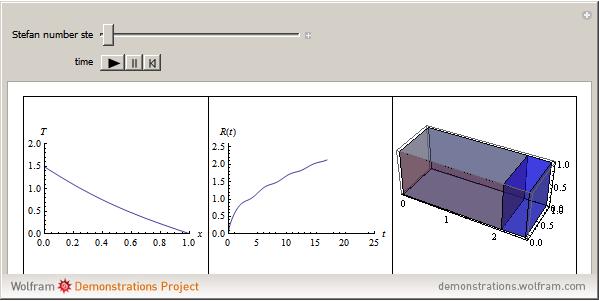
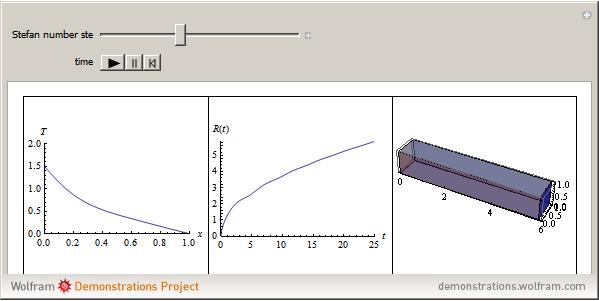
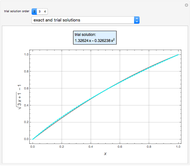
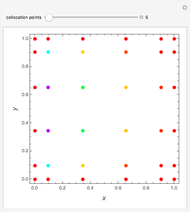
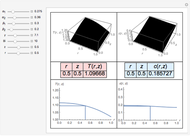
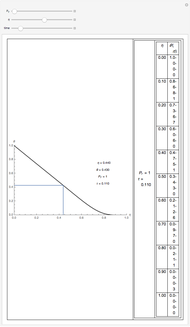
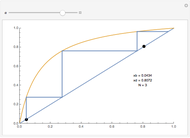
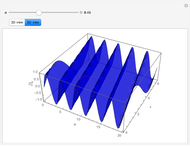
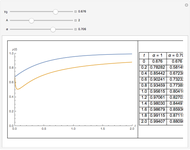
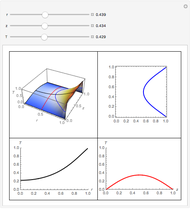
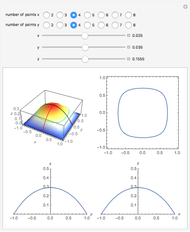
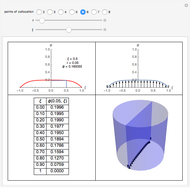
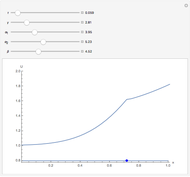
A Stefan problem is a boundary value problem for a partial differential equation in which a phase boundary can move with time. An orthogonal collocation method is used in this Demonstration to solve the one-dimensional Stefan problem with periodic boundary condition.
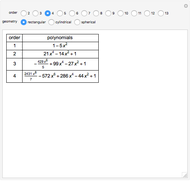
Consider the one-dimensional Stefan problem with periodic Dirichlet boundary condition. The diferential equation for this nonlinear problem, expressed in dimensionless form, is given by
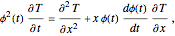
where
1) ;
2) ,
subject to initial and boundary conditions
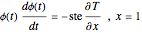3)
This problem has applications in heat and mass transfer, for example, the melting of ice, recrystallization of metals, evaporation of droplets, etc.
Reference: S. Savovic and J. Caldwell, "Finite Difference Solution of One Dimensional Stefan Problem with Periodic Boundary Conditions," International Journal of Heat and Mass Transfer, 46(15), 2003 pp. 2911–2916.
![[Snapshot]](HTMLImages/index.en/thumbnail_1.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_2.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_3.gif)
Browse all topics
