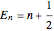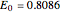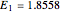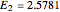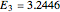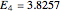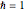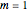Bound-State Solutions of the Schrödinger Equation by Numerical Integration

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
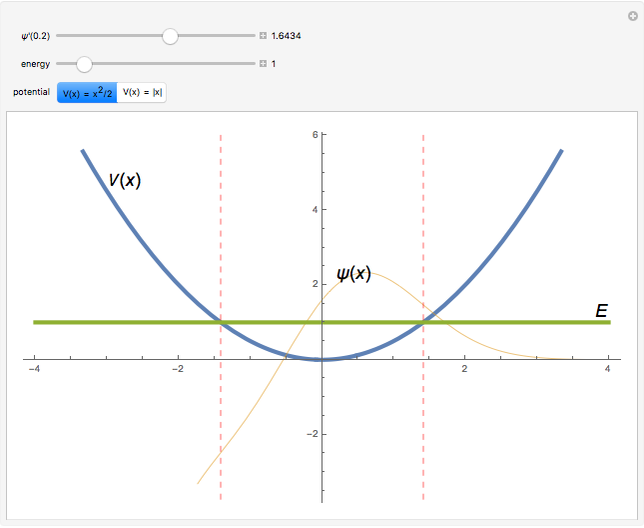
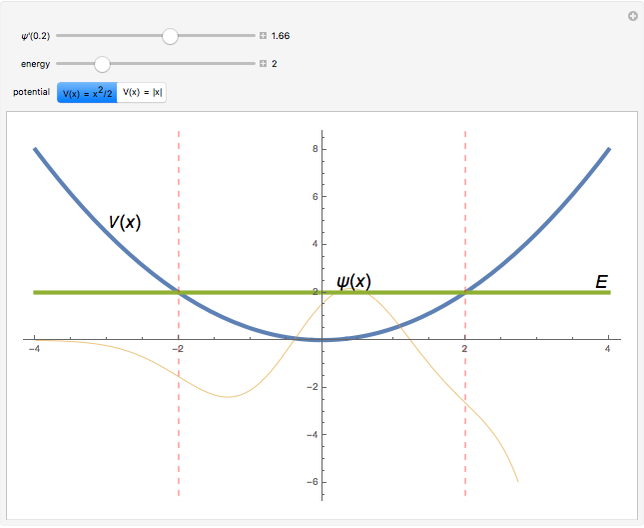
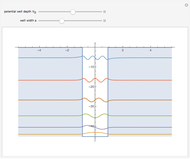
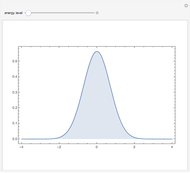
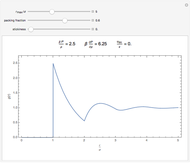
This Demonstration shows the mathematical solution of the time-independent Schrödinger equation for four potentials, the harmonic oscillator 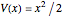 , the V-shaped potential
, the V-shaped potential 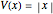 , the anharmonic oscillator
, the anharmonic oscillator 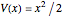
 , and a square-well potential. The wavefunction
, and a square-well potential. The wavefunction 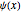 is arbitrarily fixed at
is arbitrarily fixed at 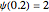 . You can obtain linearly independent solutions by numerical integration for different values of the derivative
. You can obtain linearly independent solutions by numerical integration for different values of the derivative  and the energy level
and the energy level 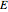 . The vertical dashed lines indicate the locations of the classical turning points.
. The vertical dashed lines indicate the locations of the classical turning points.
Contributed by: Andrés Santos
(December 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This Demonstration is inspired by section 5.7 of [1].
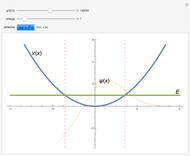
Snapshot 1: Harmonic oscillator with  . The particular solution with
. The particular solution with  behaves well in the limit as
behaves well in the limit as 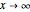 but not in the limit as
but not in the limit as  . Therefore,
. Therefore,  is not an eigenvalue.
is not an eigenvalue.
Snapshot 2: Harmonic oscillator with  . The particular solution with
. The particular solution with 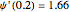 behaves well in the limit as
behaves well in the limit as  but not in the limit as
but not in the limit as 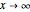 . Therefore,
. Therefore,  is not an eigenvalue.
is not an eigenvalue.
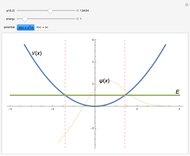
Snapshot 3: Harmonic oscillator with 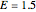 . The particular solution with
. The particular solution with 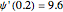 behaves well in both limits as
behaves well in both limits as 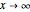 and
and  . Therefore,
. Therefore, 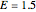 is an eigenvalue (first excited state).
is an eigenvalue (first excited state).
Snapshot 4: V-shaped potential with 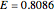 . The particular solution with
. The particular solution with  behaves well in both limits as
behaves well in both limits as 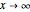 and
and  . Therefore,
. Therefore, 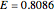 is an eigenvalue (ground state).
is an eigenvalue (ground state).
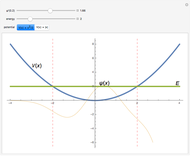
Snapshot 5: V-shaped potential with 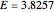 . The particular solution with
. The particular solution with 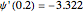 behaves well in both limits as
behaves well in both limits as 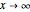 and
and  . Therefore,
. Therefore, 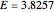 is an eigenvalue (fourth excited state).
is an eigenvalue (fourth excited state).
Reference
[1] R. Eisberg and R. Resnick, Quantum Physics of Atoms, Molecules, Solids, Nuclei, and Particles, New York: Wiley, 1985.
Permanent Citation