Steady Flow over a Rotating Disk: von Kármán Swirling Flow

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
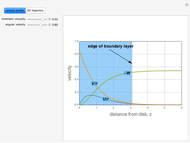
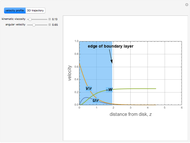
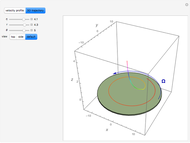
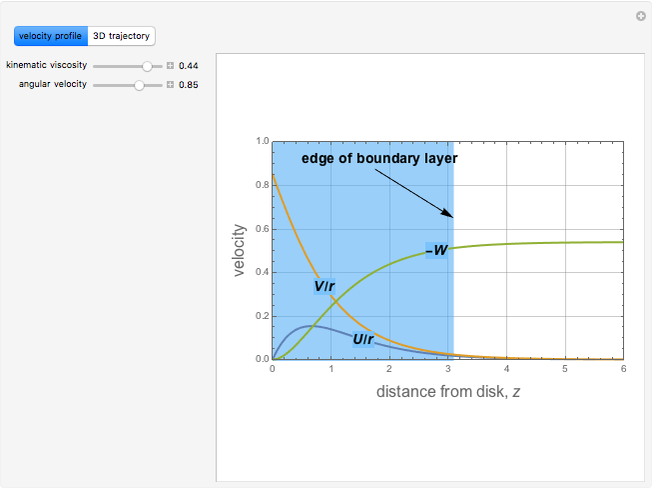
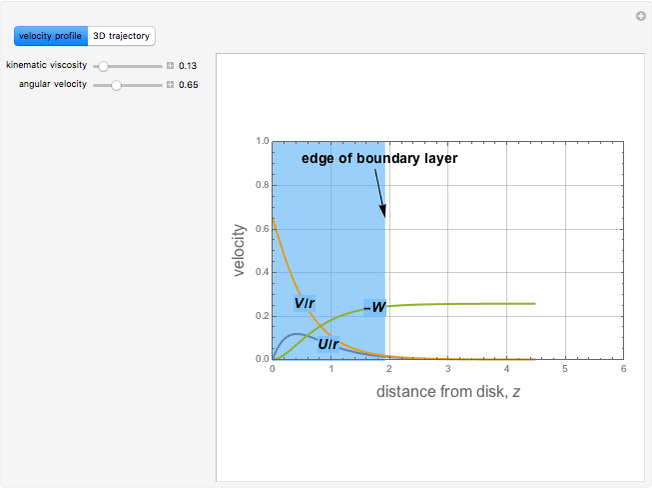
The steady flow induced by a infinite disk that rotates in its own plane at  is a classical problem in fluid mechanics. It is one of the few examples of a viscous flow that involves all three components of velocity and admits an exact solution to the Navier–Stokes equations. The velocity field for the swirling flow is given by:
is a classical problem in fluid mechanics. It is one of the few examples of a viscous flow that involves all three components of velocity and admits an exact solution to the Navier–Stokes equations. The velocity field for the swirling flow is given by:  . The Navier–Stokes equations reduce to:
. The Navier–Stokes equations reduce to:
Contributed by: Brian G. Higgins and Housam Binous (June 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] F. M. White, Viscous Fluid Flow, New York: McGraw–Hill, 1974.
[2] G. K. Batchelor, An Introduction to Fluid Dynamics, Cambridge: Cambridge University Press, 1967.
[3] H. Schlichting, Boundary-Layer Theory, 6th ed., New York: McGraw–Hill, 1968.
Permanent Citation