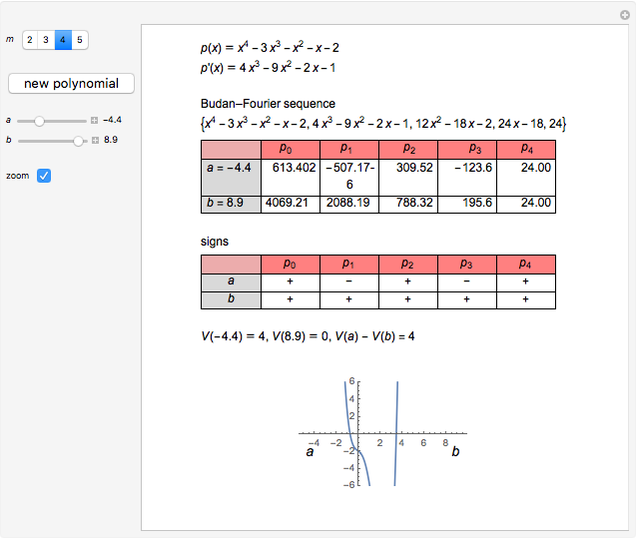
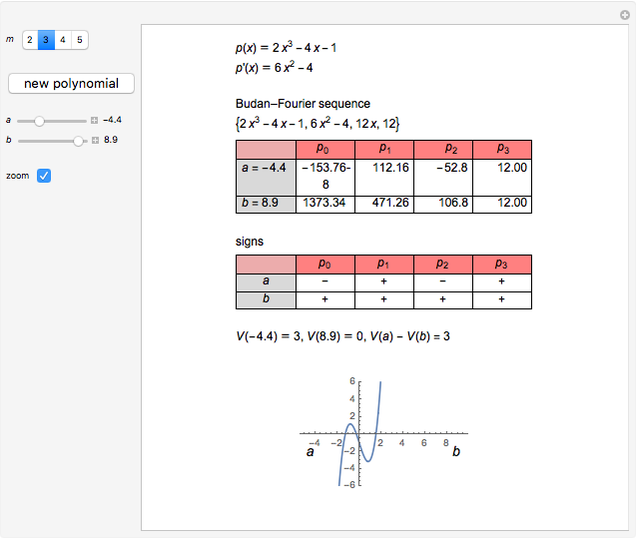
The Budan-Fourier Theorem
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
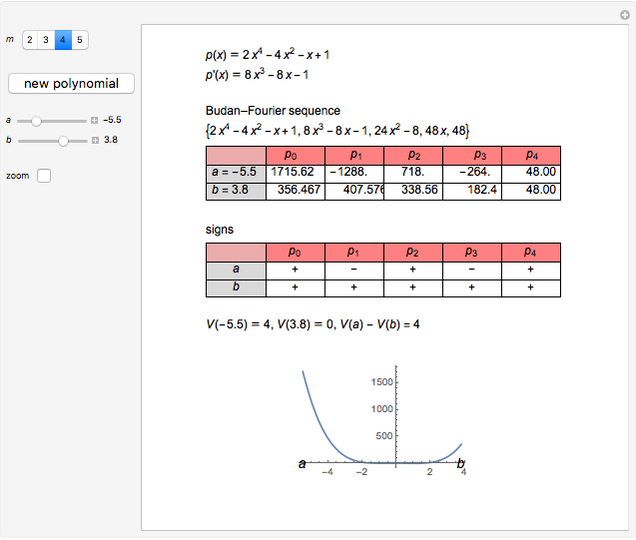
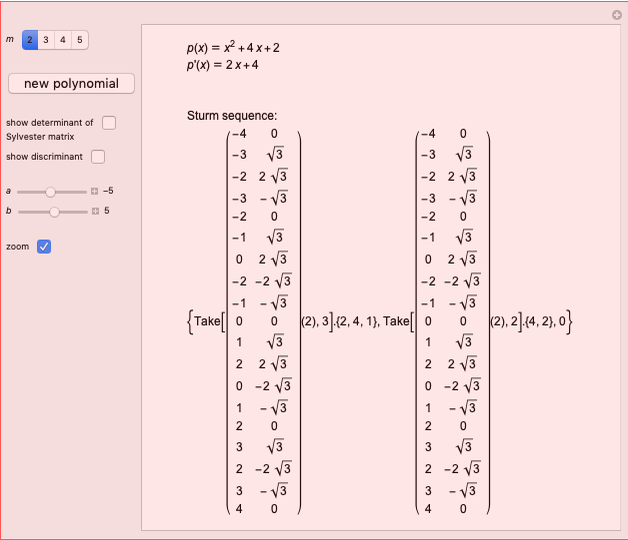
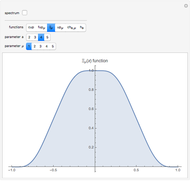
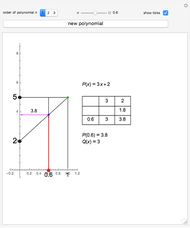
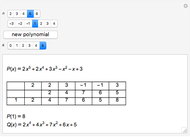
Given a polynomial  of degree
of degree  , the sequence
, the sequence  ,
,  , ...,
, ...,  is called the Budan–Fourier sequence of
is called the Budan–Fourier sequence of  .
.
Contributed by: Izidor Hafner (March 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] Wikipedia. "Budan's Theorem." (Mar 20, 2017) en.wikipedia.org/wiki/Budan's_theorem.
Permanent Citation